Binaire

[raptor77]

Bonjour chèr(e)s ami(e)s, voici un problème qui vous satisfera : Quel est le plus petit nombre entier N à k chiffres (k=2,3,4,5,6,7) dont les k premiers chiffres de la représentation binaire sont identiques à N?
amusez-vous bien :zen: merci d'avance pour vos réponses.

[aviateurpilot]

cherchant la représentation binaire de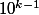
10^{k-1}=(2^3+2)^{k-1}=2^{k-1}+B2^k
or la representation binaire de 2^{k-1} et la meme que la representation de 10^{k-1} dans la base 10

et puisque tt les nombre a k chiffre >ou= 10^{k-1}

donc 10^{k-1} est le plus petit nombre dont les k premiers chiffres de la représentation binaire sont identiques a lui meme

[aviateurpilot]

cherchant la représentation binaire de

or la representation binaire de et la meme que la representation de dans la base 10

et puisque tt les nombre a k chiffre >ou=

donc est le plus petit nombre dont les k premiers chiffres de la représentation binaire sont identiques a lui meme