Trop difficile ?

[mathelot]

Bonjour,

peut-on donner cet énoncé en classe de 4ème ?

Problème Suite du Héron . Calculatrice autorisée.
Question 1
L'objet de ce problème est d'expliquer le nombre 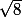. On lit ce nombre inconnu «*racine carrée de 8*». On décrit une méthode géométrique pour obtenir des valeurs décimales approchées du nombre


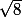
Par définition, 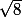cm est la longueur du côté d'un carré d'aire 8 cm2.
on doit donc vérifier l'égalité
Comment va-t-on démarrer pour obtenir des valeurs approchées de
ce nombre ?
rappel: la moyenne de deux nombres a et b est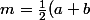
Étape 0
calculer 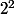et
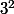
Comme le carré du nombre inconnu est 8 , et que 8 est compris entre les carrés 4 et 9, indiquer un encadrement de 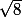entre deux nombres entiers successifs.

Etape 1
Dessiner un rectangle, d'aire 8 de longueur de côté . Que vaut la longueur 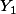de son autre côté ?
Ce rectangle a une aire de 8 cm mais n'est pas carré !
L'idée est d'obtenir un rectangle, à l'étape 2, «*plus carré*» que le rectangle de l'étape 1, tout en conservant une aire de 8 cm2.
Que vaut le produit ?
Ecrire 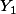comme un quotient .
Remarque : Tous les rectangles successifs ont une aire de 8 cm2.

Etape 2
Le rectangle de l'étape 2 , d'aire 8 cm2 est défini de la manière suivante:
Sa longueur de côté est la moyenne de et de .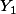
(les dimensions du rectangle de l'étape 1).
Indiquer comme une expression écrite uniquement avec la longueur .
Calculer une valeur numérique approchée,arrondie à 5 décimales, de .
Indiquer la formule du quotient pour 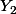sachant que l'aire du rectangle 2 vaut 8 cm2.

Etape 3
On continue....On rend le rectangle de l'étape 3 «*plus carré*» que celui de l'étape 2.
Ainsi les dimensions (longueur et largeur) des rectangles obtenus
vont être des valeurs numériques approchées de plus en plus précises du nombre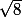
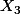est défini comme la moyenne des dimensions du rectangle de l'étape 2.
Donner l'expression de 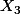écrite uniquement avec la longueur . On continue ainsi...
Indiquer des valeurs approchées (arrondies à 5 décimales) de .
Vérifier que la valeur de est proche de 8. est donc une valeur décimale approchée de
B)Question 2
On applique la méthode pour obtenir des valeurs approchées de .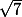
comme 4 < 7 < 9 , on pose au départ .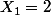
Grâce au procédé étudié question 1, donner les valeurs décimales approchées de
en conservant 5 décimales à chaque étape.
Vérification: Calculer . Le résultat doit être proche de 7.
est une valeur décimale approchée, arrondie à 5 décimales, de .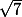

merçi pour vos conseils.

[Finrod]

[B]Problème Suite du Héron . Calculatrice autorisée.
Question 1
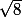
L'objet de ce problème est d'expliquer le nombre . On lit ce nombre inconnu «*racine carrée de 8*». On décrit une méthode géométrique pour obtenir des valeurs décimales approchées du nombre

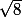
Par définition, cm est la longueur du côté d'un carré d'aire 8 cm2.
on doit donc vérifier l'égalité
Comment va-t-on démarrer pour obtenir des valeurs approchées de
ce nombre ?
rappel: la moyenne de deux nombres a et b est
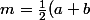Étape 0
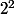
calculer et
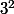
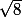
Comme le carré du nombre inconnu est 8 , et que 8 est compris entre les carrés 4 et 9, indiquer un encadrement de entre deux nombres entiers successifs.

Etape 1
Dessiner un rectangle, d'aire 8 de longueur de côté . Que vaut la longueur de son autre côté ?
Ce rectangle a une aire de mais n'est pas carré !
L'idée est d'obtenir un rectangle, à l'étape 2, «*plus carré*» que le rectangle de l'étape 1, tout en conservant une aire de 8.
Que vaut le produit ?

On peut faire une pause là déjà : c'est quoi ?

[jamys123]

yop,

tu veux faire cela en quatrième, et bien bon courage... Je te dirais, vas-y, fais-le, et tu viens nous redire comment s'était...

Comme je le dis souvent à mes stagiaires : il faut réfléchir aux objectifs visés par l'exercice...
Le maître-mot : ANALYSE A PRIORI

[mathelot]

yop,

tu veux faire cela en quatrième, et bien bon courage... Je te dirais, vas-y, fais-le, et tu viens nous redire comment s'était...

Comme je le dis souvent à mes stagiaires : il faut réfléchir aux objectifs visés par l'exercice...
Le maître-mot : ANALYSE A PRIORI

euh, j'ai corrigé l'énoncé. Il est complet.
peux tu le relire, stp ?

Le but, c'est de voir comment on obtient des valeurs approchées de

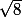
je suis d'accord avec toi. c'est quand même très technique...

jamy123, je pense que ta réponse est teintée d'ironie ? :doh:

[Finrod]

C'est surtout difficile à formuler pour de si jeunes élèves.

Moi je miserai plus sur une approche calculatoire que formaliste.
Je veux dire, plutôt que de leur faire écrire X_{2} en fonction de X_{1} avant le calcul, leur faire faire le calcul d'abord avec d'aprés etape 0, X_{1}=2 (c plus simple).
Là ça devient plus simple : Y_{1}*2=8, ils doivent trouver Y_{1}=4. Puis X_{2} est la moyenne donc c'est 3. (comme quoi c'est peut être mieux de commencer par trois).
Et ainsi de suite en donnant des valeurs approchées

Je ne dis pas qu'il faut enlever la partie formelle mais je pense que le squelette de l'exercice doit se faire avec des calculs comme ci-dessus qui leur feront moins peur. et Aprés les question avec les formules machin en fonction de chose s'ajoutent en complément.


Bon après, je donne mon point de vue mais je n'ai aucune expérience en la matière,je n'ai jamais enseigné ni en collège, ni en lycée.

[jamys123]

jamy123, je pense que ta réponse est teintée d'ironie ?

Un peu de oui, et un peu de non...

Je me base sur mon expérience, je ne connais malheureusement pas les programmes et objectifs en France, j'enseigne dans un collège CHuiCHe mais c'est quand même sensiblement pareil...

C'est vraiment une impression à chaud, c'est que l'on ne pense pas aux objectifs.

Si l'objectif est de découvrir les racines carrés et/ou les nombres irrationnels, je trouve que la méthode/exercice n'est pas bon...

Je ne pense pas que l'objectif : trouver les décimales de la racine carré de 8 fait parti du curriculum français...

[Timothé Lefebvre]

Salut,

si je peux me permettre tout dépend du degré d'intérêt des élèves pour la matière ! Si ceux-ci sont intéressés ils voudront peut-être se pencher sur le problème, si non ...

Tu peux peut-être donner ça à tes meilleurs éléments, pour tester.

[jamys123]

Salut,

si je peux me permettre tout dépend du degré d'intérêt des élèves pour la matière ! Si ceux-ci sont intéressés ils voudront peut-être se pencher sur le problème, si non ...

Tu peux peut-être donner ça à tes meilleurs éléments, pour tester.

mettons-cela sur la fougue de la jeunesse...

[Timothé Lefebvre]

Evidement, si on ne donne aux élèves que des exos basiques d'application de cours on ne risque pas d'en motiver beaucoup ... C'est avec ce genre d'exos que les élèves peuvent s'intéresser au mathématiques, peut-être plus qu'avec un exo du style "effectuer les calculs suivants : 3*(-7) ; (-4)*(-12) ; ..." (tiré d'un livre de maths de 4e) qui va bien pour les débuts du cours mais par le biais duquel on ne risque pas vraiment d'éveiller la curiosité.

N'es-tu pas d'accord avec celà ?

[jamys123]

La motivation, vaste débat...

C'est évident que "résoudre des problèmes" est plus stimulant que des "exercices rituels", n'est-ce pas l'enjeu des théories constructivistes???

Après, l'instant entre bridé et motivé les élèves est un instant infime et difficile à gérer...

Il ne faudrait pas démotiver les élèves par la difficulté des problpèmes. (Je ne serai jamais champion du monde de football bien que j'ai toute la motivation requise...)

[mathelot]

Moi je miserai plus sur une approche calculatoire que formaliste.
Je veux dire, plutôt que de leur faire écrire X_{2} en fonction de X_{1} avant le calcul, leur faire faire le calcul d'abord avec d'aprés etape 0, X_{1}=2 (c plus simple).
Là ça devient plus simple : Y_{1}*2=8, ils doivent trouver Y_{1}=4. Puis X_{2} est la moyenne donc c'est 3. (comme quoi c'est peut être mieux de commencer par trois).
Et ainsi de suite en donnant des valeurs approchées

bon, tout à fait d'accord. Je suis arrivé à la même conclusion.
La formule
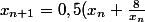est au programme de la classe de 1ère mais rien n'interdit de montrer l'algorithme sur une valeur particulière.