Un arbre se trouve au nord à 20 pas de la porte Nord, à l'extérieur de la ville. Il est visible d'un point que l'on atteint en marchant 14 pas vers le sud à partir de la porte sud puis 1775 pas vers l'ouest.
Quelles sont les dimensions de cette villes ?
1) En notant x la longueur, en pas, des côtés du carré représentant la ville, réaliser un shéma portant les indications de l'énigme.
2) a) Montrer que le problème peut se traduire par l'équation x/2/1775 = 20/x+34 (justifier soigneusement en citant le clairement le théorème utilisé.
b) Montrer que l'équation précédente se ramène a l'équation x2 +34x-71000=0.
3)Vérifier que l'équation x2 +34x-71000=0 peut s'écrire sous la forme (x-250) (x+284) =0
4) a) Soient a et b, 2 nombres réels tels que a x b = 0
Est-il possible que l'on ait en même temps a = 0 et b =0 ? Qu'en concluez vous ?
b) Appliquer ce résultat, pour résoudre l'équation (x-250) (x+284) = 0.
5) En déduire les dimensions de la ville au carrée .
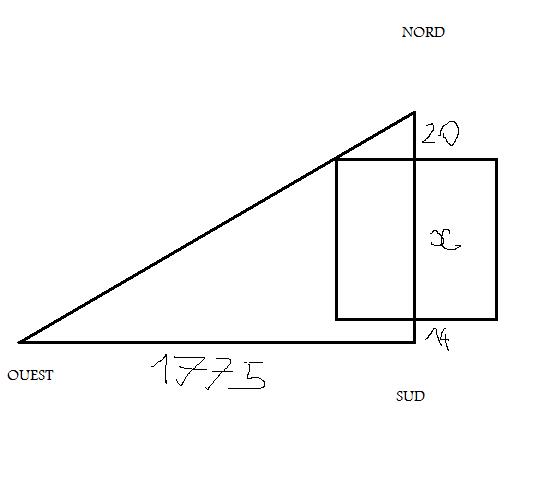
Le triangle se nomme ABC sa réduction AMN
Besoin d'aide a partir de la question 2 b)
