Bonjour à tous,
j'ai besoin d'aide svp concernant un pb de maths que je dois expliquer à mon fils de 3ème.
Il est dit dans l'énoncé :"un spirographe est constitué de roues dentées s'emboitant les unes dans les autres permettant des dessiner des arabesques . Lucie choisi une grande roue extérieure de 56 dents et une petite roue intérieure de 18 dents où elle met la mine de son crayon en A.
Combien de fois faut-il qu'elle fasse de tours de la grande roue à la petite roue pour revenir au point de départ de son dessin?
Alors j'ai cherché le diviseur commun le plus grand, j'ai trouvé 2 mais à dire vrai je ne suis pas du tout sûre ... merci pour votre point de vue
Maths 3ème-roues dentées
9 messages
- Page 1 sur 1
Re: maths 3ème-roues dentées
Salut,
Pour quelle raison choisi tu de calculer le diviseur commun le plus grand de 56 et 18 ?
Pourquoi pas la somme, ou le produit, ou... autre chose...
En bref, quel est le raisonnement que tu fait qui te conduit à penser que le diviseur commun le plus grand de 56 et 18 a quelque chose à voir avec l'énoncé ?
Pour quelle raison choisi tu de calculer le diviseur commun le plus grand de 56 et 18 ?
Pourquoi pas la somme, ou le produit, ou... autre chose...
En bref, quel est le raisonnement que tu fait qui te conduit à penser que le diviseur commun le plus grand de 56 et 18 a quelque chose à voir avec l'énoncé ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: maths 3ème-roues dentées
merci pour votre intervention, oui je ne suis pas sûre de mon pgcd
je me disais que si on suppose que la grande roue fait 1 tour complet on a 56 dents x 1 tour =56
et je cherche le nombre de tour de la petite roue dans 1 tour de grande roue soit 56/18 = 3, 11 tours
est ce ça va mieux?
je me disais que si on suppose que la grande roue fait 1 tour complet on a 56 dents x 1 tour =56
et je cherche le nombre de tour de la petite roue dans 1 tour de grande roue soit 56/18 = 3, 11 tours
est ce ça va mieux?
Re: maths 3ème-roues dentées
Effectivement, lorsque la petite roue fait un tour complet autour de la grande elle tourne sur elle même (1) de 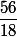 de tour (2) qui n'est pas entier (pourquoi ?) donc elle n'est pas revenue exactement à sa "position initiale".
de tour (2) qui n'est pas entier (pourquoi ?) donc elle n'est pas revenue exactement à sa "position initiale".
Et si elle fait deux tours de la grande roue, elle aura tourné de combien sur elle même ? Est-ce un nombre entier ?
Et avec trois tours ? quatre tours ? etc...
Bref, il faut combien de tours pour obtenir un nombre entier ?
(1) En fait ce n'est pas tout à fait vrai, elle fait un tour de plus lié à sa rotation autours de la grande, mais ça ne change rien.
(2) Et à priori, ce n'est pas malin du tout de l'écrire sous forme d'une approximation décimale, par contre il serait malin de l'écrire sous forme de ...
Et si elle fait deux tours de la grande roue, elle aura tourné de combien sur elle même ? Est-ce un nombre entier ?
Et avec trois tours ? quatre tours ? etc...
Bref, il faut combien de tours pour obtenir un nombre entier ?
(1) En fait ce n'est pas tout à fait vrai, elle fait un tour de plus lié à sa rotation autours de la grande, mais ça ne change rien.
(2) Et à priori, ce n'est pas malin du tout de l'écrire sous forme d'une approximation décimale, par contre il serait malin de l'écrire sous forme de ...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: maths 3ème-roues dentées
une petite anim pour illustrer, avec 27 et 12 dents
ah c'était bien le spirographe
https://melusine.eu.org/syracuse/G/pstr ... -q-9_4.gif
ah c'était bien le spirographe
https://melusine.eu.org/syracuse/G/pstr ... -q-9_4.gif
Modifié en dernier par danyL le 20 Nov 2016, 14:47, modifié 1 fois.
Re: maths 3ème-roues dentées
re-bonsoir à tous
merci pour le schéma du fonctionnement du spirographe "danyl", j'ai pu visualiser!!
Merci beaucoup Ben 314, j'ai compris et oui c'était pas très malin de calculer la fraction mais je voyais pas.
Donc je simplifie la fraction par 2, ça fait 28/9 ème ensuite je l'écris sous la forme d'une somme de fractions: 27/9 + 1/9 = 3 + 1/9 et si on multiplie ce nombre par 9 , j'obtiens un nombre entier 28.
La petite roue doit faire 9 tours de grande roue pour revenir au point de départ.
Vraiment merci et bonne soirée
merci pour le schéma du fonctionnement du spirographe "danyl", j'ai pu visualiser!!
Merci beaucoup Ben 314, j'ai compris et oui c'était pas très malin de calculer la fraction mais je voyais pas.
Donc je simplifie la fraction par 2, ça fait 28/9 ème ensuite je l'écris sous la forme d'une somme de fractions: 27/9 + 1/9 = 3 + 1/9 et si on multiplie ce nombre par 9 , j'obtiens un nombre entier 28.
La petite roue doit faire 9 tours de grande roue pour revenir au point de départ.
Vraiment merci et bonne soirée
Re: maths 3ème-roues dentées
C'est bon et en fait, le 3+1/9 ne sert pas à grand chose. Ce qui est important c'est d'écrire 56/18 sous forme irréductible vu que sous cette forme là, c'est à dire 28/9, pour "simplifier" le dénominateur, il faut absolument multiplier par 9 (ou un autre un multiple de 9) vu qu'il n'y a plus rien à simplifier entre le 28 et le 9.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: maths 3ème-roues dentées
danyL a écrit:une petite anim pour illustrer, avec 27 et 12 dents
ah c'était bien le spirographe
https://melusine.eu.org/syracuse/G/pstr ... -q-9_4.gif
sympa, l'animation !
Pour le fun, je mets ci-dessous une animation geogebra qui fait un peu pareil
Pour la démarrer, cliquer sur le bouton en bas à gauche.
On a la trace d'une hypocycloïde.(x=5/9*cos(t)+4/9*cos(5/4*t),y=5/9*sin(t)-4/9*sin(5/4*t), avec t variant de 0 à 8*pi).(pas vraiment au programme de Collège)
https://www.geogebra.org/m/qgzPRsDh
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 18 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
