Hauteur et triangle equilatéral ?

par **En-EL** » 16 Fév 2009, 16:41

Bonjour à tous,

voila un exercice avec lequel j'ai bien du mal...

" ABC est un triangle équilatéral de côté 8 cm.
[AH] est une hauteur de ce triangle.
Ecrire la longueur AH sous la forme a racine carrée de 3, avec a entier."

Je ne vois pas comment on peut calculer la hauteur AH, en sachant juste que le triangle équilatéral mesure 8 cm de côté.
De plus, comment la mettre sous la forme a racine carrée de 3?

par **oscar** » 16 Fév 2009, 16:56

Bonjour
triangle rectangle AHB; on applique Pythagore , BH = 4 et AB =8

par **En-EL** » 16 Fév 2009, 16:57

oscar a écrit:Bonjour
triangle rectangle AHB; on applique Pythagore , BH = 4 et AB =8

merci d'avoir pris le temps de lire et de répondre

Ensuite, comment pourrais-je mettre AH sous la forme a racine carré de 3 ?

par **En-EL** » 16 Fév 2009, 17:21

Il n'y a personne ? ? ? :hein:

par **oscar** » 16 Fév 2009, 17:41

As-tu fais le calcul de AH²= .....².-....²...= ......².puis V AH²

par **En-EL** » 16 Fév 2009, 17:44

oscar a écrit:As-tu fais le calcul de AH²= .....².-....²...= ......².puis V AH²

Oui je l'ai fait.
J'ai trouvé : AH = racine de 48

par **oscar** » 16 Fév 2009, 18:08

Comment trouves-tu cela: c' est Faux

Dans le triangle ABH, [AB] est l' hypoténuse et =
[BH ] est le milieu du côté soit =

Donc AH²=

.........A

B_____H_____C

par **En-EL** » 16 Fév 2009, 18:11

oscar a écrit:Comment trouves-tu cela: c' est Faux

Dans le triangle ABH, [AB] est l' hypoténuse et =
[BH ] est le milieu du côté soit =

Donc AH²=

.........A

B_____H_____C

Donc AH² = AB² - BH² ?

par **En-EL** » 16 Fév 2009, 18:17

est-ce juste au moins ?

par **Sve@r** » 16 Fév 2009, 18:18

oscar a écrit:Comment trouves-tu cela: c' est Faux

Ben non, c'est juste !!!

En-EL a écrit:Ensuite, comment pourrais-je mettre AH sous la forme a racine carré de 3 ?

En écrivant

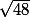
comme étant égal à

avec x² le plus grand possible. x² sortira de la racine et ça donnera en final

par **En-EL** » 16 Fév 2009, 18:19

Sve@r a écrit:Ben non, c'est juste !!!

Je me suis dit aussi :id:

J'ai bien essayé toutes les solutions!

par **En-EL** » 16 Fév 2009, 18:23

comment faire à présent, pour la mettre sous la forme de a racine de 3 ?

ahh! c'est bon j'ai trouvé!

on peut considérer ce post comme résolu.

par **Sve@r** » 16 Fév 2009, 18:36

En-EL a écrit:comment faire à présent, pour la mettre sous la forme de a racine de 3 ?

ahh! c'est bon j'ai trouvé!

Ben t'aurais pu nous l'écrire...

par **oscar** » 16 Fév 2009, 18:46

AH² = AB² - BH² = 8²-4² = 48

Tu as raison : c' est bien AH = V48 = [solution finale supprimée par la modération]

Toutes mes excuses pour mon avis erroné. Si tu avais expliqué..

Hauteur et triangle equilatéral ?

Hauteur et triangle equilatéral ?

Qui est en ligne