Exercice de géométrie (calcul d'aire)

[catamat]

Bonjour
Pour changer un petit exercice pour des élèves de collège motivés.



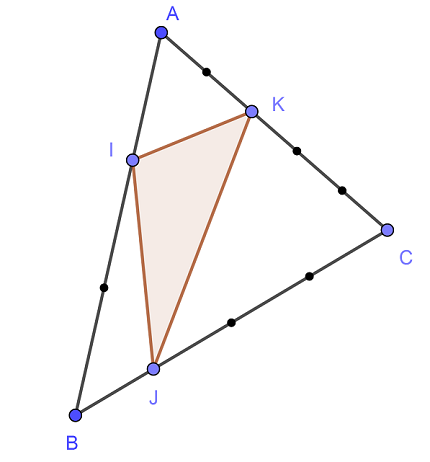
Les points sont régulièrement espacés sur les côtés du triangle, on a donc AI=1/3 AB, AK= 2/5 AC et BJ=1/4 BC.

Quelle est l'aire du triangle IJK en fonction de l'aire du triangle ABC ?

[Ben314]

Et pour les un un chouïa plus dégourdis, même question, mais sur une sphère (ou les segments sont des géodésiques bien sûr).

[catamat]

Merci Ben314 pour cette variante qui semble plus ardue...

Je rappelle que "les géodésiques sont des arcs de cercle aussi nommées arcs de grand cercle"

[Ben314]

J'ai rien fait comme calculs, mais si on prend pour argent comptant les formules de trigonométrie sphérique, on obtient rapidement une formules (à priori toute pourrie avec des fonction trigo. inverses de partout . . .)

[catamat]

Bon histoire de faire remonter un sujet de maths
On peut calculer l'aire du triangle IJK par soustraction : l'aire de ABC, notée par ex S, moins les aires des trois petits triangles calculées en fonction de S.

On a seulement besoin du th de Thalès pour exprimer les hauteurs.

[catamat]

Si H est le pied de la hauteur issue de C dans ABC et H' celui de la hauteur issue de K dans AIK les triangles AIK et ACH sont semblables dans le rapport AK/AC=2/5

L'aire de ABC est S=AB*CH/2

L'aire de AIK est AI*KH'/2=(1/3)AB*(2/5)CH/2=(1/3)*(2/5)*S=(2/15)S

[catamat]

De la même façon

aire BIJ= 1/6 S

aire CJK= 9/20 S

[catamat]

D'où l'aire de IJK = S-(2/15)S-(1/6)S-9/20)S
=S(60-8-10-27)/60
=S(15/60)
=S/4

[catamat]

Bon si on généralise un peu

Si p, q et r sont des réels éléments de ]0;1[
et I, J et K des points tels que





Quelle est l'aire du triangle IJK en fonction de p, q et r ?

[catamat]

Je vois que même ce post n'est pas épargné...

Mais bon pour le calcul d'aire la méthode est la même que dans l'exemple

[catamat]

La réponse est [pqr +(1-p)(1-q)(1-r)]S