Devoir de Recherche 3eme
Réponses à toutes vos questions du CP à la 3ème
-
Emma_Kenzo
- Membre Naturel
- Messages: 14
- Enregistré le: 30 Déc 2008, 12:45
-
 par Emma_Kenzo » 30 Déc 2008, 14:48
par Emma_Kenzo » 30 Déc 2008, 14:48
Bonjour à tous.
Ma prof de Maths a donné un devoir de recherche pour les vacances. Bien évidemment avant la leçon.
Je n'ai aucune idée de comment le résoudre :hum:
Je donne l'énoncé ci-dessous
Merci d'avance . (Je ne demande pas la réponse, juste une explication, que je puisse rédiger moi-même et ainsi comprendre quelque chose . lol)
Cliquez sur la miniature pour l'agrandir. ^^

 par busard_des_roseaux » 30 Déc 2008, 14:54
par busard_des_roseaux » 30 Déc 2008, 14:54
euh, un devoir de recherche, c'est fait ...pour chercher.
ceci écrit, trace la parallèle à l'horizontale (AB) passant par D.
elle coupe (BC) en X.
l'inconnue est la distance CX.
les triangles ABC et ECD sont résolubles (on peut calculer tous les angles
et tous les côtés).
évalue l'angle DCX . Comme on connait la distance DC, DCX devient un triangle résoluble.
-
yvelines78
- Membre Légendaire
- Messages: 6903
- Enregistré le: 15 Fév 2006, 21:14
-
 par yvelines78 » 30 Déc 2008, 14:57
par yvelines78 » 30 Déc 2008, 14:57
bonjour,
il n'est pas évident sur ta figure que beta=150°!!!!
-
Emma_Kenzo
- Membre Naturel
- Messages: 14
- Enregistré le: 30 Déc 2008, 12:45
-
 par Emma_Kenzo » 30 Déc 2008, 15:04
par Emma_Kenzo » 30 Déc 2008, 15:04
Désolée . lol . beta = 15°
-
yvelines78
- Membre Légendaire
- Messages: 6903
- Enregistré le: 15 Fév 2006, 21:14
-
 par yvelines78 » 30 Déc 2008, 15:13
par yvelines78 » 30 Déc 2008, 15:13
prolonge (BC)
trace la // à (AB) passant par D
F leur point de concours
calcule la valeur de l'angle DCF (BCF=180°)
applique la trigo dans le triangle rect DCF
-
Emma_Kenzo
- Membre Naturel
- Messages: 14
- Enregistré le: 30 Déc 2008, 12:45
-
 par Emma_Kenzo » 30 Déc 2008, 15:26
par Emma_Kenzo » 30 Déc 2008, 15:26
Je suis désolée je suis vraiment nulle en maths . lol
Comment est-ce que peux calculer la valeur de l'angle DCF ?
-
yvelines78
- Membre Légendaire
- Messages: 6903
- Enregistré le: 15 Fév 2006, 21:14
-
 par yvelines78 » 30 Déc 2008, 15:34
par yvelines78 » 30 Déc 2008, 15:34
calcule la valeur de l'angle DCF (BCF=180°)
DCE=90°
calcule ACB (ACB triangle rect+CAB=30°)
-
Emma_Kenzo
- Membre Naturel
- Messages: 14
- Enregistré le: 30 Déc 2008, 12:45
-
 par Emma_Kenzo » 30 Déc 2008, 17:00
par Emma_Kenzo » 30 Déc 2008, 17:00
Merci =) . Au final, ça donne ça :
Je trace la droite (d), parallèle à (AB) : elle coupe (BC) en F.
Calcul de l'angle ACB :Dans le triangle ACB rectangle en B, on a :
cos


BC / AC
cos


173,2 / 346,4
cos


0,5
;)  60 °Calcul de l'angle DCF :
60 °Calcul de l'angle DCF :On sait que BCF = 180°
BCF = ACB + ECD +
DCFBCF = 60° + 90° +
DCFDCF = BCF - ACB + ECD
DCF = 180° - 150°
DCF = 30°Calcul de FC :Dans le triangle DCF rectangle en F, on a :
cos


FC / DC
cos 30°

FC / 20,4
FC

cos 30° x 20,4
FC  17,6 mCalcul de [FB] :
17,6 mCalcul de [FB] :FB

173,2 + 17,6
FB  190,8 mLe dénivelé 2 mesure 190,8 mètres.
190,8 mLe dénivelé 2 mesure 190,8 mètres.
-
yvelines78
- Membre Légendaire
- Messages: 6903
- Enregistré le: 15 Fév 2006, 21:14
-
 par yvelines78 » 30 Déc 2008, 17:09
par yvelines78 » 30 Déc 2008, 17:09
Emma_Kenzo a écrit:Merci =) . Au final, ça donne ça :
Je trace la droite (d), parallèle à (AB)
passant par D : elle coupe (BC) en F.
Calcul de l'angle ACB :Dans le triangle ACB rectangle en B, on a :
cos


BC / AC
cos


173,2 / 346,4
cos


0,5
;)  60 °il y a plus simple et plus exact, les angles aigus d'un triangles rect sont complémentairesCalcul de l'angle DCF :
60 °il y a plus simple et plus exact, les angles aigus d'un triangles rect sont complémentairesCalcul de l'angle DCF :On sait que BCF = 180°
BCF = ACB + ECD +
DCFBCF = 60° + 90° +
DCFDCF = BCF - ACB + ECD
DCF = 180° - 150°
DCF = 30°Calcul de FC :Dans le triangle DCF rectangle en F, on a :
cos


FC / DC
cos 30°

FC / 20,4
FC

cos 30° x 20,4
FC  17,7 mCalcul de [FB] :
17,7 mCalcul de [FB] :FB

173,2 + 17,
7FB  190,9 mLe dénivelé 2 mesure 190,9 mètres.
190,9 mLe dénivelé 2 mesure 190,9 mètres.
est-cequ'on dit si on arrondi au mètre?
cela semblerait logique dans ce genre de mesure
-
Emma_Kenzo
- Membre Naturel
- Messages: 14
- Enregistré le: 30 Déc 2008, 12:45
-
 par Emma_Kenzo » 30 Déc 2008, 17:11
par Emma_Kenzo » 30 Déc 2008, 17:11
elle ne demande pas d'arrondir, elle demande juste :
Déterminer le dénivelé 2.
Merci . J'ai enfin réusssi =D
-
mathelot
 par mathelot » 30 Déc 2008, 17:28
par mathelot » 30 Déc 2008, 17:28
Salut,
avec les données


AB=300m
ED=79m
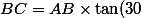)
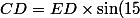)
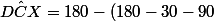-90=30)
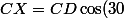 = ED \sin(15) \cos(30))
calcul de la valeur exacte de sin(15)
sin(15)=sin(60-45)=sin(60) cos(45)- cos(60) sin(45)
tous les coups sont permis
lire ici=\frac{\sqrt{3}}{2} \frac{\sqrt{2}}{2} -\frac{1}{2} \frac{\sqrt{2}}{2})
=\frac{\sqrt{2} \left( \sqrt{3}-1 \right)}{4})
\cos(30) =\frac{\sqrt{2} \left( \sqrt{3}-1 \right)}{4} \times \frac{\sqrt{3}}{2})
\cos(30) =\frac{\sqrt{2} \left(3- \sqrt{3}\right)}{8})
dénivellé
}{8})
application numérique:
dénivellé=191 mètres s'il s'agit d'une piste de ski
s'il s'agit d'un accélérateur d'électrons, tu peux calculer le dénivellé en
Angstroms :zen:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 18 invités

