Défi avec un nombre entier
17 messages
- Page 1 sur 1
Défi avec un nombre entier
Bonjour,
J'ai cet exercice à faire pour mon DM:
-je suis un nombre entier
-je suis un carré
-je suis un cube
-je suis supérieur à 100 mais inférieur à 1000
On dit qu'il n'y en a pas deux comme moi.
Est-ce exact?
Je suis perdu,j'avais pensé au chiffre 1 car le carré de 1=1 et le cube de 1=1 mais je bloque à la 3eme affirmation : supérieur à 100 mais inférieur à 1000???
Merci pour votre aide.
J'ai cet exercice à faire pour mon DM:
-je suis un nombre entier
-je suis un carré
-je suis un cube
-je suis supérieur à 100 mais inférieur à 1000
On dit qu'il n'y en a pas deux comme moi.
Est-ce exact?
Je suis perdu,j'avais pensé au chiffre 1 car le carré de 1=1 et le cube de 1=1 mais je bloque à la 3eme affirmation : supérieur à 100 mais inférieur à 1000???
Merci pour votre aide.
Re: Défi avec un nombre entier
Salut, quand on dit que le nombre est un carré sa veut dire que par exemple si X est le nombre qui répond à ses conditions bha on a X=a² où a est un entier et de même si X est un cube sa veut dire qu'il existe un b entier tel que X=b^3 (enfin je pense)
Bon j'ai essayé comme un idiot tout les carré de 10 à 27 et j'ai trouvé que 729 répondait a ses conditions.
On a 729=27² et 729=9^3.
Voila j'espère ne pas m'être trompé.
PS: En fait, j'ai commencer à 10 car le nombre doit être plus grand que 100
Bon j'ai essayé comme un idiot tout les carré de 10 à 27 et j'ai trouvé que 729 répondait a ses conditions.
On a 729=27² et 729=9^3.
Voila j'espère ne pas m'être trompé.
PS: En fait, j'ai commencer à 10 car le nombre doit être plus grand que 100
Re: Défi avec un nombre entier
On pose X le nombre qui répond a ses conditions et les entiers a et b tel que X=a² et X=b^3.
En fait en y réfléchissant un peu pour limiter les choix du nombre tu sais qu'on doit avoir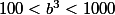 Comme la fonction cube est croissante R (même strictement) on a
Comme la fonction cube est croissante R (même strictement) on a
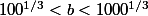
Et sa te limite à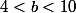
Une fois que tu auras tout essayé tu verra que le seul qui peut marcher c'est pour b = 9 , donc le nombre solution est 9^3=729.
En fait en y réfléchissant un peu pour limiter les choix du nombre tu sais qu'on doit avoir
Et sa te limite à
Une fois que tu auras tout essayé tu verra que le seul qui peut marcher c'est pour b = 9 , donc le nombre solution est 9^3=729.
Re: Défi avec un nombre entier
Salut,
Voici les cubes des 10 premiers entiers naturels:
1 a pour cube 1
2 a pour cube 8
3 a pour cube 27
4 a pour cube 64
5 a pour cube 125
6 a pour cube 216
7 a pour cube 343
8 a pour cube 512
9 a pour cube 729
10 a pour cube 1000
Seuls ceux entre 100 et 1000 conviennent 125, 216, 343, 512,729,1000
De plus on sait que tout carré parfait a pour chiffre des unités {0;1;4;9;5}
Il reste uniquement 125, 216, 729,1000
Lequel est un carré? Il suffit de regarder si leur racine carrée est un entier..
Voici les cubes des 10 premiers entiers naturels:
1 a pour cube 1
2 a pour cube 8
3 a pour cube 27
4 a pour cube 64
5 a pour cube 125
6 a pour cube 216
7 a pour cube 343
8 a pour cube 512
9 a pour cube 729
10 a pour cube 1000
Seuls ceux entre 100 et 1000 conviennent 125, 216, 343, 512,729,1000
De plus on sait que tout carré parfait a pour chiffre des unités {0;1;4;9;5}
Il reste uniquement 125, 216, 729,1000
Lequel est un carré? Il suffit de regarder si leur racine carrée est un entier..
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Défi avec un nombre entier
Bonjour,
Si ce nombre est à la fois un carré et un cube (a^2 et b^3), c'est qu'il est une puissance de 6.
Des puissances de 6 comprises entre 100 et 1000, il n'y en a pas des tonnes : 1^6, 2^6, 3^6, ... .
Si ce nombre est à la fois un carré et un cube (a^2 et b^3), c'est qu'il est une puissance de 6.
Des puissances de 6 comprises entre 100 et 1000, il n'y en a pas des tonnes : 1^6, 2^6, 3^6, ... .
Re: Défi avec un nombre entier
le problème faut aller le chercher, le provoquer, aller jusqu'à ses limites.
on me dit je suis un carré et je suis un cube.
le premier truc à évoquer, rah l'autre ç'est pas possible:
5x5 est un carré
5x5x5 est un cube
si j'en ai deux des 5 je ne peux pas en avoir 3
rah l'autre encore une erreur d'énoncé
Arrivé à ce stade, si tu ne trouves pas tu vas diner.
Et tu reviens après le diner.
il me faut du trruc fois deux et du truc fois trois, hum, hum, du 2 et du 3
Du 2 et du 3, il ya bien le 6 qui fait ça.
Donc on essaye:
5x5x5x5x5x5
et là bingo
j'ai un cube : (5x5) x (5x5) x (5x5)
j'ai un carré: (5x5x5) x (5x5x5)
Reste plus qu'a essayer:
avec le un on va pas loin
avec le deux c'est bien trop peu
avec le trois , là j'y crois
avec le quatre, ça va trop loin
hé,hé , grillé par pseuda!
on me dit je suis un carré et je suis un cube.
le premier truc à évoquer, rah l'autre ç'est pas possible:
5x5 est un carré
5x5x5 est un cube
si j'en ai deux des 5 je ne peux pas en avoir 3
rah l'autre encore une erreur d'énoncé
Arrivé à ce stade, si tu ne trouves pas tu vas diner.
Et tu reviens après le diner.
il me faut du trruc fois deux et du truc fois trois, hum, hum, du 2 et du 3
Du 2 et du 3, il ya bien le 6 qui fait ça.
Donc on essaye:
5x5x5x5x5x5
et là bingo
j'ai un cube : (5x5) x (5x5) x (5x5)
j'ai un carré: (5x5x5) x (5x5x5)
Reste plus qu'a essayer:
avec le un on va pas loin
avec le deux c'est bien trop peu
avec le trois , là j'y crois
avec le quatre, ça va trop loin
hé,hé , grillé par pseuda!
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Défi avec un nombre entier
Bonjour Beagle,
Suivie de près. C'est ça, il faut être une puissance de 6 pour être à la fois un carré et un cube : à démontrer (mais pas au collège).
Suivie de près. C'est ça, il faut être une puissance de 6 pour être à la fois un carré et un cube : à démontrer (mais pas au collège).
Re: Défi avec un nombre entier
Pseuda a écrit:Bonjour Beagle,
Suivie de près. C'est ça, il faut être une puissance de 6 pour être à la fois un carré et un cube : à démontrer (mais pas au collège).
Bonjour Pseuda
Pour démontrer faut décomposition en facteurs premiers.Je ne sais pas quelle année on bosse ça.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Défi avec un nombre entier
Merci les amis pour votre aide,je trouve cet exercice costaud au vue de vos réponses, je ne suis qu'en 3eme...
Re: Défi avec un nombre entier
La solution de Lostounet à 2h44 du matin est tout à fait niveau collège.
Re: Défi avec un nombre entier
pascal16 a écrit:La solution de Lostounet à 2h44 du matin est tout à fait niveau collège.
Quelle honte, Pascal, quelle honte.
Privilégier une solution de sortie de boites de nuit,
alors que d'honnêtes gens comme Pseuda et Beagle envoient des solutions du dimanche matin avant la messe.Je suis dégouté!
Bon, sinon, on apprend en troisième le PGCD, on apprend les puissances? le carré et le cube seulement?
Et on n'apprend pas la décomposition en facteurs premiers!!!!!
Possible me rappelle plus du tout ce que j'ai fait avec ma fille et quand!
parce que si on apprend les puissances, le nombre de fois de la multiplication s'additionne, se retranche,
bon ben je crois que l'exo aurait sa place comme on l'a fait avec Pseuda.Pour avoir du 2 et du 3 on a cela quand 6, c'est un challenge qui me parait jouable.
Ensuite qu'il n' ai qu'une seule solution, avec rigueur difficile, mais bon si on est parti j'ai besoin de puissance 6, et alors entre 2 et 4 il n' y a que 3, on ne peut pas trouver d'autres entiers.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Défi avec un nombre entier
pascal16 a écrit:La solution de Lostounet à 2h44 du matin est tout à fait niveau collège.
Bonsoir,
Encore faut-il savoir qu'un carré se termine par certains chiffres et pas d'autres. Au collège je ne vois qu'une solution : aligner les carrés, aligner les cubes, .... avec peut-être quelques raccourcis.
Mais on peut aussi avoir l'intuition des puissances de 6.
Re: Défi avec un nombre entier
en fait, on peut supprimer cette allusion à la terminaison des carrés
soit au final : "
Voici les cubes des 10 premiers entiers naturels:
1 a pour cube 1
2 a pour cube 8
3 a pour cube 27
4 a pour cube 64
5 a pour cube 125
6 a pour cube 216
7 a pour cube 343
8 a pour cube 512
9 a pour cube 729
10 a pour cube 1000
Seuls ceux entre 100 et 1000 conviennent 125, 216, 343, 512,729,1000
Lequel est un carré? Il suffit de regarder si leur racine carrée est un entier..
"
soit au final : "
Voici les cubes des 10 premiers entiers naturels:
1 a pour cube 1
2 a pour cube 8
3 a pour cube 27
4 a pour cube 64
5 a pour cube 125
6 a pour cube 216
7 a pour cube 343
8 a pour cube 512
9 a pour cube 729
10 a pour cube 1000
Seuls ceux entre 100 et 1000 conviennent 125, 216, 343, 512,729,1000
Lequel est un carré? Il suffit de regarder si leur racine carrée est un entier..
"
Re: Défi avec un nombre entier
Le tout avec la calculatrice bien sûr. Mais c'est pas grave, le but est déjà de les faire jouer avec les puissances.
Re: Défi avec un nombre entier
on va quand même pas sortir un programme scratch avec le chat qui fait miaou quand la solution est trouvée !
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
