Blockage dans des mises en équation.

[MATH&ME]

Salut à tous .

A) Une pochette contient 4 catégories de piéces de monnais:
1/3 "de la pochette" > "piéces" de 10
1/4 > de 5
1/6 > de 1
6 pieces de (1/2)
Quel est le nombre exacte de chaque catégorie.
Quel est le nombre exacte d'argent au total dans la pochette.
Alors pour celle ci l'inconnue est le nombre de pieces :
10x+5x+1x+(1/2)x = 1/3+1/4+1/6+(6 pieces (1/4) je pense)


B) Un prof a promis a un éleve de lui donner 8 euros pour chaque probléme résolu correctement , et lui prendre 5 euros pour chaque probléme non résolu ou faux .
Aprés avoir fait les 26 problémes , l'argent donnée est égale à l'argent prise .
26 =8x+5x ??

C) Des amies veulent acheter une PSP , Mais chacun doit donner 6 euros.
Mais 3 parmi eux n'ont pas pus participer .
Alors on a décidé d'augmenter la mise de 1.5 euros pour chacun.
Quel est le prix de la PSP ??
j'ai mis :
x = prix PSP ; y = Nombre de participants .
x = (y-3)(6+1.5) ????

D) Celle ci elle est plus avancée pour moi mais j'éspére la comprendre quand méme .
Alors une voiture part de A vers B à 8h à une vitesse de 64 km/h
Une moto part de B vers A à 9h à une vitesse de 36 km/h
Si la distance entre A et B est 239 Km ; donner l'heure et la position de croisement des 2 véhicules

Merci d'avance .

[C.Ret]

Bonjour,

1)
Dans cet énoncé, il y a deux équations.
Pour faciliter les choses appelons N le nombre total de pièces dans la pochette et S la somme d'argent que cela représente.
Saurais-tu écrire chacune des équations permetant d'exprimer pour N et S les données du problème ?

2)
Là aussi, il faut diffèrencier les diffèrents objets du problème.
Il y a d'un coté le nombre d'excercices réalisés dont une partie est juste et l'autre fausse ou non résolue.
De l'autre coté, il y a les sommes d'argent gagnées ou perdues.


3)
Bien, mais ici aussi tu ne retranscrit qu'une partie des informations de l'énoncé.
N'y a-t-il pas une seconde façon d'exprimer le prix x de la PSP.


4)
Là aussi, ,on demande deux choses, l'heure de la rencontre de l'auto et de la moto et le lieu.

[mouette 22]

Salut à tous .

A) Une pochette contient 4 catégories de piéces de monnais:
1/3 "de la pochette" > "piéces" de 10
1/4 > de 5
1/6 > de 1
6 pieces de (1/2)
Quel est le nombre exacte de chaque catégorie.
Quel est le nombre exacte d'argent au total dans la pochette.
Alors pour celle ci l'inconnue est le nombre de pieces :
10x+5x+1x+(1/2)x = 1/3+1/4+1/6+(6 pieces (1/4) je pense)


B) Un prof a promis a un éleve de lui donner 8 euros pour chaque probléme résolu correctement , et lui prendre 5 euros pour chaque probléme non résolu ou faux .
Aprés avoir fait les 26 problémes , l'argent donnée est égale à l'argent prise .
26 =8x+5x ??

C) Des amies veulent acheter une PSP , Mais chacun doit donner 6 euros.
Mais 3 parmi eux n'ont pas pus participer .
Alors on a décidé d'augmenter la mise de 1.5 euros pour chacun.
Quel est le prix de la PSP ??
j'ai mis :
x = prix PSP ; y = Nombre de participants .
x = (y-3)(6+1.5) ????

D) Celle ci elle est plus avancée pour moi mais j'éspére la comprendre quand méme .
Alors une voiture part de A vers B à 8h à une vitesse de 64 km/h
Une moto part de B vers A à 9h à une vitesse de 36 km/h
Si la distance entre A et B est 239 Km ; donner l'heure et la position de croisement des 2 véhicules

Merci d'avance .

pour ton dernier problème il faut connaitre les formules avec TEMPS VITESSE et DISTANCE

D=V*T
D/V=T
D/T=V

la voiture sera en C à 9h elle aura parcouru 64km.
A 9h quelle distance sépare la moto et la voiture ?
si tu appelles x le kilometrage de la voiture combien de km pour la moto?

la suite est donc simple ..

[C.Ret]

la suite est donc simple ..

C'est le très classique problème du chez de gare ! :lol3:

[MATH&ME]

Bonjour,

1)
Dans cet énoncé, il y a deux équations.
Pour faciliter les choses appelons N le nombre total de pièces dans la pochette et S la somme d'argent que cela représente.
Saurais-tu écrire chacune des équations permetant d'exprimer pour N et S les données du problème ?

n10+n5+n1+n(1/2) = S

[C.Ret]

n10+n5+n1+n(1/2) = S

:doh:
Oula Oula c'est quoi toutes ces variables n10, n5, n1 et n(1/2) ?
En général, on n'écrit pas une équation sans expliqué un peu ce que représente chaque variable.


:we:
Ensuite, pour retranscrire les données, j'ai déjà expliqué qu'il devait y avoir deux équations.
Deux équation ça veut dire deux signes égal.


:zen:
Ensuite chez moi ici il y a un dicton local qui sert bien lorsque l'on veux organiser les choses :
"On ne mélange pas les chiffons et les torchons".

:go: Ce qui veux dire dans notre cas, on ne mélange pas les nombres de pièce et les sommes d'argent.
On ne peux pas avoir de part et d'autre du signe égal des objets de nature diffèrente. On dit en mathématiques qu'il faut des équations homogènes.

:lol3:
Donc j'attend deux équations, l'une concernant le nombre de pièces dans la pochette:
N = ....

Et là, on pourra en expliquant un petit peu éventuellement faire intervenir des variables supplèmentaires pour désigner le nombre de chaque pièce (n10, n5, n1 ...)

Et l'autre concernant la somme d'argent dans la pochette :
S = ....

Et là il n'y aura que des sommes. Par exemple si n10 est le nombre de pièce de 10€, alors on ne devrait y voir quelque chose comme (10*n10) qui est bien homogène à une somme d'argent.

[mouette 22]

Salut à tous .

A) Une pochette contient 4 catégories de piéces de monnais:
1/3 "de la pochette" > "piéces" de 10
1/4 > de 5
1/6 > de 1
6 pieces de (1/2)
Quel est le nombre exacte de chaque catégorie.
Quel est le nombre exacte d'argent au total dans la pochette.
Alors pour celle ci l'inconnue est le nombre de pieces :
10x+5x+1x+(1/2)x = 1/3+1/4+1/6+(6 pieces (1/4) je pense)


B) Un prof a promis a un éleve de lui donner 8 euros pour chaque probléme résolu correctement , et lui prendre 5 euros pour chaque probléme non résolu ou faux .
Aprés avoir fait les 26 problémes , l'argent donnée est égale à l'argent prise .
26 =8x+5x ??

C) Des amies veulent acheter une PSP , Mais chacun doit donner 6 euros.
Mais 3 parmi eux n'ont pas pus participer .
Alors on a décidé d'augmenter la mise de 1.5 euros pour chacun.
Quel est le prix de la PSP ??
j'ai mis :
x = prix PSP ; y = Nombre de participants .
x = (y-3)(6+1.5) ????

D) Celle ci elle est plus avancée pour moi mais j'éspére la comprendre quand méme .
Alors une voiture part de A vers B à 8h à une vitesse de 64 km/h
Une moto part de B vers A à 9h à une vitesse de 36 km/h
Si la distance entre A et B est 239 Km ; donner l'heure et la position de croisement des 2 véhicules

Merci d'avance .

allons y clairement et simplement :happy2: pour ton exercice 1
soit x le nombre de pièces
si x/4+x/3+x/6 représentent les pièces de 10et 5et 1 ça fait un total de 9x/12

ce qui veut dire que les 3x/12 qui restent représentent les 6 pièces de 0,50(de dirhams :lol3: ou d'euros...)
ça va tu continues ?

ce travail fait, il te sera facile de calculer la somme que représente ces pièces

[MATH&ME]

Enfait ce probleme commence vraiment à me jouer sur les nerfs .
Pour la premiere parti de l'équation .
x = la somme d'argent .
Alors :
x/3+x/4+x/6 = 9x/12
x/4 = 6*0.50 dh
d'ou x/4 = 3 * 1dh ?? ??
Est ce ca la méthode ?.

[mouette 22]

[quote="MATH&ME"]Enfait ce probleme commence vraiment à me jouer sur les nerfs .
Pour la premiere parti de l'équation .
x = la somme d'argent .
Alors :
x/3+x/4+x/6 = 9x/12
x/4 = 6*0.50 dh
d'ou x/4 = 3 * 1dh ?? ?? [HTML]
Est ce ca la méthode ?.[[/HTML]/QUOTE]

IL FAUT D'ABORD CALCULER LE NOMBRE DE PIECES... ON NE S'OCCUPE PAS DE LA VALEUR
SI tu lis ATTENTIVEMENT le problème on te parle de """PIECES... ""quand tu auras trouvé les pieces de 5et de 10.et de 1. tu pourras alors trouver facilement ce que représentent ces pièces en VALEUR

9x/12 représente les pieces de 5, de 10et de 1

le reste """12x/12 moins 9x/12"""" soit 3x/12 représente les pièces de 0,50
on te dit dans le texte que le reste c'est 6pièces de 0,50
donc ton equation c'est 3x/12=6
donc x =24
il ya 24pieces
dont 1/3de pièces de 10 . Soit 8pièces de 10 dont la valeur est 80 dh (si on veut :lol3: )
1/4 de pièces de 5..soit 6pièces ... donc 30dh
1/6 de pièces de 1..soit 4pieces... donc 4dh
et enfin 6pièces de 0,50 soit 3dh
tu n'as plus qu à faire le total... As tu compris ?

[C.Ret]

Pour le 1)

Mise en équation

Soit N le nombre de pièces dans la pochette.

Appelons le nombre de pièces de 10 $
Appelons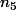 le nombre de pièces de 5 $.
Appelons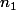 le nombre de pièces de 1 $.
Et appelons le nombre de pièce de 1/2 $.

On a donc , le total de pièces qui est donné par N ( Il ya au total N pièces dans la pochette).


L'énoncé nous donne les proportions des trois premières catégorie de pièces :
Les pièces de 10 $ reprèsent 1/3 du total des pièces de la pochette d'où on peut écrire :
Les pièces de 5 $ représente 1/4 du total des pièces, donc on écrit
Les pièces de 1 $ représente 1/6 du total de pièces, d'où
On nous dit qu'il y a 6 pièces d'un 1/2 $, on note donc

On peut donc faire disparaitre nos varaibles intermédiaires n10, n5, n1 et nc dont on a plus besoin :


:+:


Maintenant que l'on a bien posé le problème et trouvé l'équation pour le nombre de pièces, on peut compter la somme d'argent.

Appelons S la somme d'argent dans la pochette. La somme dans la pochette est la somme de la valeur de chaque pièce multipliée par le nombre de pièces.
S'il ya deux pièce de 10 $, il y aura une somme de 2x10=20 $, etc.

Donc, on peut écrire que la somme totale S dans la pochette est :


Or, d'après ce que l'on a fait ci-dessus, on sait exprimer chaque nombre de picèe en fonction de N le nombre de pièces total dans la pochettes. On remplace donc et on obtient :

:++:

On peut factoriser par N:

Et simplifier :



Pour trouver S, on résout d'abors la première équation qui donnera N et on remplacera dans cette seconde équation.


Application Numérique

Pour déterminer numériquement N, il suffit de résoudre cette première équation.
On simplifie cette expression pour ne voir apparaitre N qu'une seule fois :


IL ya donc 24 pièces dans la pochette.

On remplace N dans la seconde équation


Pour trouver S= 117$.

[MATH&ME]

Merci infiniment maintenant les choses sont plus claires .
Enfait cret ; la méthode la plus facil est la méthode numérique , plus pratique et facile à comprendre .

[MATH&ME]

Pour la 2éme maitenant j'ai imaginé ca :
26 *(1/(-5x)) = 26*(1/8x) ???

[mouette 22]

Pour la 2éme maitenant j'ai imaginé ca :
26 *(1/(-5x)) = 26*(1/8x) ???

non ton équation est fausse.Il y a 26exercices en tout. La somme des réponses justes et fausses =26


tu commets la même erreur que pour les pièces et la valeur des pièces dans le premier problème .

[MATH&ME]

Alors :
26 x = (26-x)(-5)+(26-x)(+8) ???

[mouette 22]

Alors :
26 x = (26-x)(-5)+(26-x)(+8) ???

pourquoi mets tu 26-x pour les deux ?

l'un est x les réponses positives

l'autre (26-x) les réponses négatives



il aura donc 8x pour les bonnes réponses et 5(26-x) pour les mauvaise

et on te dit que c'est EGAL
alors ecris le que c'est egal!!


tu dois trouver 10 séances positives et 16 séances négatives .

[MATH&ME]

Merci mouette22 , j'admet que ne suis pas fort en mise en équations , les problèmes étaient mon point faible de puis longtemps .
Si tu a des conseils comme des méthodes standards à suivre dans tout problèmes et leurs mise en équations surtout ça serai sympa .

D'une autre part je vais essayer avec l’exercice 3 .

[Lostounet]

Salut,

Check this si tu veux: http://www.maths-forum.com/showpost.php?p=684862&postcount=14
Y'a deux problèmes

[MATH&ME]

Alors pour la 3éme j'ai la somme initiale de la PSP qu'est : 6x , et on n'auras la même somme avec 3 personnes de moin CAD : (6+1.5)(x-3)
Alors l'équation est 6x = 7.5x-22.5
22.5 = 7.5x-6x = 1.5x
x= 15
Somme est (15-3)(7.5) = 90 avec 3 personnes de moin
6*15 = 90 avec 6 personnes .
Ca demande juste un bon resonnement.

[MATH&ME]

Yo thanks Mr loostonet , exactly what i need .

[mouette 22]

Alors pour la 3éme j'ai la somme initiale de la PSP qu'est : 6x , et on n'auras la même somme avec 3 personnes de moin CAD : (6+1.5)(x-3)
Alors l'équation est 6x = 7.5x-22.5
22.5 = 7.5x-6x = 1.5x
x= 15
Somme est (15-3)(7.5) = 90 avec 3 personnes de moin
6*15 = 90 avec 6 personnes .
Ca demande juste un bon resonnement.

oui un bon ""raisonnement "(raison :lol3: )