Mouette22 , SVP , il me reste sulement la derniére et je términe cette leçon .
T ( voiture) = D/V = 239/64 = 3.734375 h
T ( moto) = 239/36 = 6.6388888 h
Alors :
La voiture Arrivra à B à : 11.734375 (h)
La moto arrivera à A à : 15.6388888 (h)
Maintenant comment coordonner ces données en forme d'équation , et comment savoir le lieu et le temps de croisement .????
Blockage dans des mises en équation.
33 messages
- Page 2 sur 2 - 1, 2
[quote="MATH&ME"]Mouette22 , SVP , il me reste sulemh ent la derniére et je términe cette leçon .
T ( voiture) = D/V = 239/64 = 3.734375 h
T ( moto) = 239/36 = 6.6388888 h
Chan 79 te donne la solution rapide au problème
à 9h la voiture a fait 64km il reste à faire 175km
a chaque heure moto et voiture font 64+36=100km
pour faire 175 km ils leur faut ( 175*60)/100= 105minutes soit 1h45
donc ils se rencontrent à10h45
reste le trajet de la voiture en 2h45 et de la moto en 1h 45
T ( voiture) = D/V = 239/64 = 3.734375 h
T ( moto) = 239/36 = 6.6388888 h
Chan 79 te donne la solution rapide au problème
à 9h la voiture a fait 64km il reste à faire 175km
a chaque heure moto et voiture font 64+36=100km
pour faire 175 km ils leur faut ( 175*60)/100= 105minutes soit 1h45
donc ils se rencontrent à10h45
reste le trajet de la voiture en 2h45 et de la moto en 1h 45
mouette 22 a écrit:oui mais on ne te demande pas ça"""""les heures d'arrivée en A"ou B!!! """"
as tu fait un shéma ? ça aide beaucoup!moi je ne peux pas te le transmettre ça dépasse mes compétences informatiques!!!!!
La voiture partant à 8h elle aura fait 64km quand il sera 9h .Elle sera en C (dessine STP!)
le temps mis juqu"au point de rencontre sera le MËME pour la voiture et la moto
Le parcours est de 175km.... (distance totale moins 64...
soit x ce que parcourt la voiture
la moto fera 175-x
temps mis par la voiture pour faire x, x/64
temps mis par la moto pour faire 175-x , (175-x)/39
exprime que ces deux temps sont égaux , c'est ton équation:
x/64= (175-x)/39
103x=11200
ce qui fait 1h 48mn(verifie stp). C'est le temps qu'il faut ajouter à 9h pour avoir l'heure de croisement . Il sera donc 10h 48mn
il te reste à connaitre les distances parcourues par l'un et par l'autre ça c'est simple . La voiture a roulé pendant 1h48+1h soit 2h48 à 64km à l'heure . tu calcules ce qu elle a parcouru
La moto a roulé seulement 1h48 à 39kmh... calcule également ce qu elle a parcouru
(verifie le temps je ne suis pas très douée j'ai laissé tomber les secondes ce qui n'est pas normal!!! :hum: )
Bonjour
on peut aussi se dire que toutes les heures, la distance qui sépare les véhicules diminue de 64+36 soit 100 km
Comme, à partir de 9 h, ils sont séparés de 239-64 soit 175 km, ils se croiseront à 9h +175/100 h soit 9h +1.75 h soit 9 h + 1h 45 min soit 10 h 45 min
chan79 a écrit:Bonjour
on peut aussi se dire que toutes les heures, la distance qui sépare les véhicules diminue de 64+36 soit 100 km
Comme, à partir de 9 h, ils sont séparés de 239-64 soit 175 km, ils se croiseront à 9h +175/100 h soit 9h +1.75 h soit 9 h + 1h 45 min soit 10 h 45 min
c'est certainement vrai! :happy2:
et plus rapide comme solution !
J'apprécie l'aide .
Mais j'ai une autre vision pour ca :
Alors :
Pour la voiture :
9h = 64 km parcourue .
Moto = pour savoir à quelle heure la moto aura parcouru 64 km , j'ai mis une petite méthode .
10 h = 36 km parcourue .
x = 64 km
x = (64*10)/36
x = 17.77 h
Alors pour la moto , elle aura parcourue 64 km à l'heure 17.77
Est ce que cette demarche mene à quelque chose ???
Mais j'ai une autre vision pour ca :
Alors :
Pour la voiture :
9h = 64 km parcourue .
Moto = pour savoir à quelle heure la moto aura parcouru 64 km , j'ai mis une petite méthode .
10 h = 36 km parcourue .
x = 64 km
x = (64*10)/36
x = 17.77 h
Alors pour la moto , elle aura parcourue 64 km à l'heure 17.77
Est ce que cette demarche mene à quelque chose ???
MATH&ME a écrit:J'apprécie l'aide .
Mais j'ai une autre vision pour ca :
Alors :
Pour la voiture :
9h = 64 km parcourue .
Moto = pour savoir à quelle heure la moto aura parcouru 64 km , j'ai mis une petite méthode .
10 h = 36 km parcourue .
x = 64 km
x = (64*10)/36
x = 17.77 h
Alors pour la moto , elle aura parcourue 64 km à l'heure 17.77
Est ce que cette demarche mene à quelque chose ???
mais 17h77 c'est une drôle d'heure :lol3: !et si la moto n'a fait que 64kmà 17heures hou la la c'est une tortue !!!! elle est partie à 9h ... et tu dis à 17h elle n'a fait que 64km????? tu ne crois pas que c'est faux ?
MATH&ME a écrit:Euuh nn , elle parcoure 64 en 1.77 h alors à 10.77
:marteau:
mais c'est quoi cette heure ? au Maroc non plus on ne dépasse pas les 60mn!!!! :ptdr:
lis ce qu à écrit CHANT.. c'est super interessan t
chaque heure ils se rapprochent de 64+36=100KM
en combien de temps se rapprocheront ils pour faire 175km ?
(175 *60)/100=105mn soit 1h45
donc à 9h+1h45= 10h45 c'est l'heure de la rencontre!
après tu te débrouilles c'est simple de chercher ce que chacun a parcouru.(tu dois trouver 176pour la voiture et 63pour la moto... total 239)
Pour la 2)
VAriables et équations
Choix des variables et inconnues:
Soit le nombre de questions posées à l'élève.
le nombre de questions posées à l'élève.
Soit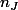 le nombre de réponses Justes données par l'élève.
le nombre de réponses Justes données par l'élève.
Soit le nombre de réponses Fausse données par l'élève.
le nombre de réponses Fausse données par l'élève.
Soit la somme d'argent gagnée par l'élève.
la somme d'argent gagnée par l'élève.
Mise en équation :
L'élève répond aux questions, les répondes qu'il donne sont soit justes, soit fausses:
questions, les répondes qu'il donne sont soit justes, soit fausses:

A chaque réponse juste, l'élève gagne 8 $ et il perd 5 $ s'il se trompe ou ne répond pas, la somme d'argent lui appartenant après avoir répondu juste à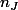 questions et faux à
questions et faux à  est donc :
est donc :

Résolution de l'équation :
Après avoir répondu à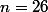 questions, l'élève n'a pas gagné ni perdu d'argent, la somme
questions, l'élève n'a pas gagné ni perdu d'argent, la somme 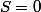 :
:
En en déduit que

On remplace dans l'expression de la somme :
dans l'expression de la somme :
\\8 \times n_J &=& 5\times 26 \,-\, 5\times n_J \\ 8 \times n_J \,+\, 5\times n_J &=& 5\times 26 \\ n_J \times (8+5) &=& 5\times 26 \\ n_J \times 13 &=& 130 \\ n_J &=& \frac{130}{13}\\ n_J&=&10 \end{matrix})
D'où

Vérification des résultats
L'élève a répondu à 26 questions.
10 seulement de ses réponses étaient justes. Il a donc donné 16 réponses fausses.
Le maitre lui a donc donné $ pour les 10 réponses justes.
$ pour les 10 réponses justes.
Mais il lui a repris $ pour les 16 réponses fausses.
$ pour les 16 réponses fausses.
A la fin des 26 questions, l'élève n'a rien gagné (ni perdu d'ailleurs).
VAriables et équations
Choix des variables et inconnues:
Soit
Soit
Soit
Soit
Mise en équation :
L'élève répond aux
A chaque réponse juste, l'élève gagne 8 $ et il perd 5 $ s'il se trompe ou ne répond pas, la somme d'argent lui appartenant après avoir répondu juste à
Résolution de l'équation :
Après avoir répondu à
En en déduit que
On remplace
D'où
Vérification des résultats
L'élève a répondu à 26 questions.
10 seulement de ses réponses étaient justes. Il a donc donné 16 réponses fausses.
Le maitre lui a donc donné
Mais il lui a repris
A la fin des 26 questions, l'élève n'a rien gagné (ni perdu d'ailleurs).
Merci j'ai deja reussi à resoudre ls trois premiers .
Alors pour la troisieme.
J'ai suivie cette methode qui repose sur les regles de D/V/t
Alors pour savoir l'heure de rencontre il faut tout d'abord unifier les temps de depart .
Alors la distance se diminuera .
239 - 64 (64 = distance parcourue entre 8h t 9h )
Alors la distance unifieé seras 175
D= 175 km
v1 = 64
v2 = 36
Th = 175/(64+36)
= 1.75 = 1h45min
Alors le temps de croisement seras = 10h45min
Pour le lieu de croisement :
D1 = 64 km*1.75h = 112km
D2 = 36 km*1.75h = 63
Alors revenont au temps initial de 8h
D1 = 112 km + 64 km = 176 km
D2 = 63 km
D1+D2 = 239 km
Alors il se croiseront à 176 km de A et 63 Km de B .
Alors pour la troisieme.
J'ai suivie cette methode qui repose sur les regles de D/V/t
Alors pour savoir l'heure de rencontre il faut tout d'abord unifier les temps de depart .
Alors la distance se diminuera .
239 - 64 (64 = distance parcourue entre 8h t 9h )
Alors la distance unifieé seras 175
D= 175 km
v1 = 64
v2 = 36
Th = 175/(64+36)
= 1.75 = 1h45min
Alors le temps de croisement seras = 10h45min
Pour le lieu de croisement :
D1 = 64 km*1.75h = 112km
D2 = 36 km*1.75h = 63
Alors revenont au temps initial de 8h
D1 = 112 km + 64 km = 176 km
D2 = 63 km
D1+D2 = 239 km
Alors il se croiseront à 176 km de A et 63 Km de B .
Très bien.
Félicitations.
Le plus dur c'est de faire les premiers. Après, on prend l'habitude de poser les problèmes en équations et de les résoudre. Alors, on peut s'attaquer à des problèmes de plus en plus complexes! :we:
Avec l'expérience, on fini aussi par chercher à utiliser la méthode la "plus simple" ou la "plus rapide" ce qui permet de traiter des problèmes plus complexes et surtout de faire beaucoup plus vite.
Par exemple, on peut traiter le problème du "chef de gare" sans faire de réduction des distances ou d'unification des temps. Il suffit simplement de ne pas oublier de tenir du compte du temps de trajet plus court de la moto en écrivant la distance parcourrue. C'est à dire en faisant la difèrence entre temps de parcours et heure de la journée.
La rencontre de l'auto et la moto a lieu après un temps de parcours pour l'auto. Elle aura parcourue la distance
pour l'auto. Elle aura parcourue la distance  où
où 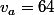 km/h.
km/h.
La moto partant une heure plus tard, elle aura au moment de la rencontre parcourru une distance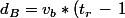) avec
avec 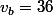 km/h.
km/h.
La distance séparant A de B étant AB=239 km, on a au moment de la rencontre :
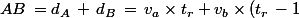)
soit
On obtient
On en déduit que la rencontre a lieu à 10h45, que la voiture aura parcourru 176 km (après un parcours de 2.75 h) et la moto 63 km (après 1.75 h de trajet).
On a bien 176+63=239 km.
C'est une question d'habitude ou de préfèrence, on peut travailler en utilisant les heures de la journée dans les équation, ou ne le faire qu'en transformant au moment de résumer les résultats les temps de parcours en horaires.
Cela vaut aussi pour les autres excercice, les équations proposées ne sont pas les seules possibles, il y a souvent pluseurs façon de poser un même problème. C'est pour cela qu'il est important de bien expliquer et nommer les variables et ce que l'on fait.
:lol3:
Félicitations.
Le plus dur c'est de faire les premiers. Après, on prend l'habitude de poser les problèmes en équations et de les résoudre. Alors, on peut s'attaquer à des problèmes de plus en plus complexes! :we:
Avec l'expérience, on fini aussi par chercher à utiliser la méthode la "plus simple" ou la "plus rapide" ce qui permet de traiter des problèmes plus complexes et surtout de faire beaucoup plus vite.
Par exemple, on peut traiter le problème du "chef de gare" sans faire de réduction des distances ou d'unification des temps. Il suffit simplement de ne pas oublier de tenir du compte du temps de trajet plus court de la moto en écrivant la distance parcourrue. C'est à dire en faisant la difèrence entre temps de parcours et heure de la journée.
La rencontre de l'auto et la moto a lieu après un temps de parcours
La moto partant une heure plus tard, elle aura au moment de la rencontre parcourru une distance
La distance séparant A de B étant AB=239 km, on a au moment de la rencontre :
soit
On obtient
On en déduit que la rencontre a lieu à 10h45, que la voiture aura parcourru 176 km (après un parcours de 2.75 h) et la moto 63 km (après 1.75 h de trajet).
On a bien 176+63=239 km.
C'est une question d'habitude ou de préfèrence, on peut travailler en utilisant les heures de la journée dans les équation, ou ne le faire qu'en transformant au moment de résumer les résultats les temps de parcours en horaires.
Cela vaut aussi pour les autres excercice, les équations proposées ne sont pas les seules possibles, il y a souvent pluseurs façon de poser un même problème. C'est pour cela qu'il est important de bien expliquer et nommer les variables et ce que l'on fait.
:lol3:
Merci Cret et mouette pour vos explications .
J'ai compris aussi qu'il faut non seulement savoir poser une equation , mais savoir créer des méthodes personelles tout en utilisant les relations , ce qui demande une bonne comprehention du probléme .
La difficultés reside dans la détéction et la création des relations entre les inconnus et les élément du probléme .
J'ai compris aussi qu'il faut non seulement savoir poser une equation , mais savoir créer des méthodes personelles tout en utilisant les relations , ce qui demande une bonne comprehention du probléme .
La difficultés reside dans la détéction et la création des relations entre les inconnus et les élément du probléme .
MATH&ME a écrit:Merci Cret et mouette pour vos explications .
J'ai compris aussi qu'il faut non seulement savoir poser une equation , mais savoir créer des méthodes personelles tout en utilisant les relations , ce qui demande une bonne comprehention du probléme .
La difficultés reside dans la détéction et la création des relations entre les inconnus et les élément du probléme .
et CHAN 79 surtout . .....
J'estime que si on a du mal en mathématiques c'est pas les explications "" tape à l'oeil ""et compliquées qui peuvent aider . :lol3:. Tu as raison lire et relire ton texte pour bien comprendre ce qu on te demande .
33 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
