3ème - dm n°11

[bebe60]

Bonjour,
Ma fille a ce DM à faire et elle ne comprend rien et je ne peut hélas l’aider mes études en math sont trop loin, auriez-vous la gentillesse de m’aider à trouver les réponses à ce DM.

Voici le lien du DM

http://gmallet42.free.fr/3eme_2010_2011_DM11_angle_inscrit_polygone_regulier.pdf


En vous remerciant par avance de vos réponses rapides.
Bien cordialement

[takezo]

Bonjour,


Exercice 1.
Question 1.a
Les points A et M sont sur le cercle, O est son centre : les segments[OA] et [OM] et sont donc deux rayons du cercle.
Que peut-on donc dire des longueurs OA et OM ?
Maintenant la nature du triangle MOA devrait vous être connue...
Réponses ?

1. b) Dans un triangle de cette nature, que peut-on dire alors des angles à la base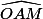 et ?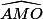

Question 2.
Les points M et B sont sur le cercle et O en est le centre... etc.
Vous avez donc les réponses du 2. grâce au 1.

La dernière question n'est pas aussi "évidente" que les deux premières...
Quand on fait la somme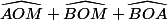 , il n'a pas dû vous échapper qu'on faisait "un tour complet"... Ce qui représente combien de degrés ?
On a donc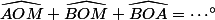 (1)

La somme des mesures des angles d'un triangle vaut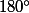
Donc dans le triangle AOM :

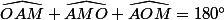
Et on en déduit :
(2)
Mais dans ce trianglke, on sait que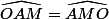

Donc :


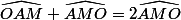
que je remplace dans l'égalité (2) pour obtenir :


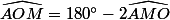
On procède à l'identique dans le triangle MOB...
On trouve ?

On remplace dans l'égalité (1)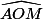 et 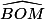par les expressions qu'on vient de trouver...

Et on obtient ?

On commence par là, ensuite au vu de vos réponses on terminera cet exercice...

Bye

[bebe60]

Bonjour,

Merci de votre aide mais pour quelqu'un qui n'est absolument pas matheux cela donne quoi en Français ? :ptdr:
je suis désolée mais je suis nulle !!! et je n'ai rien compris

[takezo]

Bonsoir,

Ce n'est pas un Problème de nullité....
Je suis désolé à mon tour, mais un problème de Maths, ne se résout pas seulement en faisant de belles phrases !
Ensuite, si Maman n'a pas les connaissances (et on ne peut vous le reprocher :id:), sa fille, elle, est censée les avoir.

L'exercice 1 est une démonstration du théorème de "l'angle inscrit" qui se voit en 3e..
Adoncques, Mademoiselle votre fille, étant en 3e, elle est passée successivement par les classes de 6e, 5e et 4e, n'est-ce pas ? :lol3:
Elle est donc censée pouvoir répondre aux questions que j'ai posées.
Vous devriez lui passer le relais :zen:
Parce que quand je demande de comparer les longueurs de 2 rayons d'un cercle (c'est du programme de 6e), il n'y a que 2 réponses possibles : ou elles sont égales ou elles ne le sont pas...
Alors, réponse ?
Ensuite nature du triangle.
Ce triangle a un nom bien précis :
isocèle, équilatéral, rectangle ou rectangle et isocèle répondant à des définitions bien précises aussi.
Alors à quel type de triangle a-t-on affaire ?

On commence par là, on poursuivre avec les réponses obtenues : cela évitera que vous ayez l'impression qu'on joue aux devinettes.

Courage ! Seule la question 3 est "un peu" technique et là ça risque d'être difficile à passer.
On va faire ça en tranches aussi fines que possible...

Bye