Tétraèdre

[Scytale222]

Un matheux sympa pour m'expliquer ou me guider vers:
Connaissant les coordonnées de trois sommets et du centre d'un tétraèdre régulier (ça se dit ?), peut-on calculer les coordonnées du quatrième sommet ?

[capitaine nuggets]

Salut !

Connaissant trois des quatre points d'un tétraèdre régulier, on peut trouver le quatrième et ainsi trouver le centre de ce tétraèdre.

Pour comprendre, une (possible) analogie consiste à dire que si, dans le plan, tu connais deux des trois points d'un triangle équilatéral, tu peux trouver le troisième et donc trouver le centre de ce triangle.

Appelons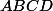 le tétraèdre régulier. Supposons connus , et . Puisque 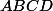est supposé être régulier, le point appartient à la droite 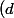orthogonale au plan passant par le centre du triangle (équilatéral) , et vérifie 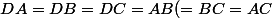. Il restera à montrer que le centre du tétraèdre 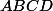est tel que 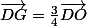(il me semble).

[chan79]

Un matheux sympa pour m'expliquer ou me guider vers:
Connaissant les coordonnées de trois sommets et du centre d'un tétraèdre régulier (ça se dit ?), peut-on calculer les coordonnées du quatrième sommet ?

Salut
Juste une remarque:
Connaissant 3 sommets, il y a deux possibilités pour le quatrième.
Les 3 points sont connus comment ? Par leurs coordonnées ?

[Scytale222]

Merci pour les explications, je vais essayer de digérer tout cela. @ Cap Nuggets, mais j'ai besoin des coordonnées de D, pas seulement de construire graphiquement le tétraèdre.

@Chan
Oui; on connaît les coordonnées de trois sommets et du centre ( A= (Ax; Ay; Az) etc..). Et on peut connaître la longueur des segments (si nécéssaire) AB, BC,AC et OA, OB, OC ainsi que, je suppose, OD puisque le tétraèdre es supposé régulier. (O=centre du tétraèdre.)
Y at-t-il moyen de calculer ?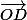
(O= origine et centre du tétraèdre).

[Scytale222]

Quel fouillis mon énoncé . J'essaye de formuler le problème autrement.

Soit le tétraèdre régulier ABCD de centre M dans un repère orthonormé x, y, z d'origine O.

Nous connaissons:
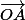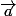= (ax, ay, az)
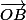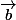= (bx, by, bz)
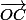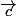= (cx, cy, cz)
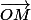= (mx, my, mz)

Calculer = (? ? ?)

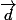Je ne sais pas si c'est mieux ainsi...

Ou peut-être en utilisant le centre M, connu du tétra ?

= + +

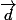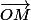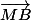... si

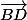= , ce que je n'arrive pas à visualiser. (C'est dur d' être nul en maths, croyez-moi !)

[Ben314]

Salut,
Le "centre" d'un polyèdre (et d'un polygone) en général, ça ne veut rien dire vu qu'il y a plusieurs points susceptibles d'être appelés "le centre" (l'isobarycentre des sommets, le centre de gravité du polyèdre massif, les éventuels centres de la sphère inscrite ou circonscrite, etc...) sauf que dans le cas d'un tétraèdre régulier, tout ces points sont les mêmes donc il n'y a pas d'ambiguïté.
En particulier le "centre" c'est l'isobarycentre des sommets donc ce qui te donne de façon immédiate les coordonnées du point D en fonction de celles de A,B,C et M.

[Scytale222]

Merci Ben ! J'aurais dû y penser ! Comme dans la molécule de CH4... Stable car les vecteurs des liaisons carbone-hydrogène s'annulent.(..je crois.)
A présent le plus dur... L' algèbre. Mettre tout ça en équations.

=

4mx-ax-bx-cx = dx
4my-ay-by-cy = dy
4mz-az-bz-cz = dz

J'imagine que c"est quelque chose ainsi ? Ou bien j'ai tout faux ?
(amusant comme tout ce latex ! J'ai au moins appris quelque chose bien que ces vecteurs en colonne ressemblent plus à des matrices... )