Le produit de 2 nombres négatifs donne un nombre positif : c
14 messages
- Page 1 sur 1
le produit de 2 nombres négatifs donne un nombre positif : c
Bonjour les ami(e)s ma question est peut-être un peu bête mais comment fait-on pour démontrer que le produit de nombres négatifs donne un nombre positif?(ex:(-3)*(-2)=6)
Merci d'avance pour votre réponse.
Cordialement.
raptor.
Merci d'avance pour votre réponse.
Cordialement.
raptor.
Bonjour
(-3)*(-2)=(-1)*(-1)*3*2 (par commutativité et associativité de la multiplication)
d'où :
(-3)*(-2)=1*3*2=6
L'idée est de se dire qu'un nombre est négatif s'il est l'opposé d'un nombre positif.
La multiplication par -1 peut être considérer comme un opérateur permettant de passer d'un nombre à son opposé, d'où le résultat.
(-3)*(-2)=(-1)*(-1)*3*2 (par commutativité et associativité de la multiplication)
d'où :
(-3)*(-2)=1*3*2=6
L'idée est de se dire qu'un nombre est négatif s'il est l'opposé d'un nombre positif.
La multiplication par -1 peut être considérer comme un opérateur permettant de passer d'un nombre à son opposé, d'où le résultat.
Salut,
l'absence de démonstration avait indigné le jeune Stendhal. En représentant le produit de 2 réels par un rectangle on peut, et c'est même assez naturel si on pense au déterminant de 2 vecteurs de R² on peut avoir une illustration de la chose.
Le signe de "l'aire" d'un rectangle est donné par le sens de parcourt autour du rectangle.
Plus pour le sens direct
Moins pour le sens rétrograde.
Il est facile de vérifier sur un dessin que -x- et +x+ donnent le même sens de parcourt.
Ce n'est en aucun cas une démonstration, mais c'est une idée sur ce qui ce passe.
A+
l'absence de démonstration avait indigné le jeune Stendhal. En représentant le produit de 2 réels par un rectangle on peut, et c'est même assez naturel si on pense au déterminant de 2 vecteurs de R² on peut avoir une illustration de la chose.
Le signe de "l'aire" d'un rectangle est donné par le sens de parcourt autour du rectangle.
Plus pour le sens direct
Moins pour le sens rétrograde.
Il est facile de vérifier sur un dessin que -x- et +x+ donnent le même sens de parcourt.
Ce n'est en aucun cas une démonstration, mais c'est une idée sur ce qui ce passe.
A+
Faisons simple:
1° étape: Démontrer que y(-x)=-yx
Nous savons que y(x+z)=yx+yz
Prenons z=-x
On a donc y(x-x)=yx+y(-x)
soit 0=yx+y(-x)
après une soustraction de yx dans les deux membres, on obtient:
-yx=y(-x)
2° étape:Démontrer que vx=(-v)*(-x)
Reprenons notre calcul à la ligne 0=yx+y(-x)
Prenons y=-v
On obtient 0=x(-v)+(-v)*(-x)
On utilise la relation x(-v)=-xv puis on ajoute xv aux deux membres de l'équation.
On obtient xv=(-x)*(-v)
CQFD
1° étape: Démontrer que y(-x)=-yx
Nous savons que y(x+z)=yx+yz
Prenons z=-x
On a donc y(x-x)=yx+y(-x)
soit 0=yx+y(-x)
après une soustraction de yx dans les deux membres, on obtient:
-yx=y(-x)
2° étape:Démontrer que vx=(-v)*(-x)
Reprenons notre calcul à la ligne 0=yx+y(-x)
Prenons y=-v
On obtient 0=x(-v)+(-v)*(-x)
On utilise la relation x(-v)=-xv puis on ajoute xv aux deux membres de l'équation.
On obtient xv=(-x)*(-v)
CQFD
Le mieux est de rappeler clairement la caractérisation des réels positifs.
La définition de la relation d'ordre dépend de la construction choisie des réels. Dans tous les cas, elle découle de celle dans . Cependant une caractérisation (indépendante de la construction, heureusement) peut-être donnée, et est donnée pour une définition axiomatique des réels.
. Cependant une caractérisation (indépendante de la construction, heureusement) peut-être donnée, et est donnée pour une définition axiomatique des réels.
Pour\in\mathbb{R}^2) ,
, 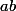 équivaut à
équivaut à 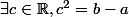 .
.
A partir de là, on peut démontrer le résultat voulu sans argument autophage du type "un négatif est l'opposé d'un positif" où sans avoir à recourir à beaucoup de lignes pour cacher un vide... Montrer que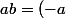(-b)) ne sert que si l'on peut prouver la nature de l'un des deux membres de l'égalité.
ne sert que si l'on peut prouver la nature de l'un des deux membres de l'égalité.
La définition de la relation d'ordre dépend de la construction choisie des réels. Dans tous les cas, elle découle de celle dans
Pour
A partir de là, on peut démontrer le résultat voulu sans argument autophage du type "un négatif est l'opposé d'un positif" où sans avoir à recourir à beaucoup de lignes pour cacher un vide... Montrer que
Sinon on peut faire la construction de  comme suit :
comme suit :
Sur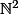 on considère la relation
on considère la relation  définie par
définie par R(c;d)) ssi
ssi 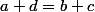 .
.
On montre facilement que c'est une relation d'équivalence.
En pratique) est un représentant de
est un représentant de 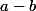 .
.  \in {\mathbb{N}}^2\text{, } a-b \in\mathbb{Z}) .
.
Ceci étant fait on défini le produit par\times (c\,;\,d) =(ac+bd\,;\,ad+bc)) .
.
On vérifie facilement que cette opération est compatible avec la relation , et la règle des signes en découle tout naturellement.
, et la règle des signes en découle tout naturellement.
Sur
On montre facilement que c'est une relation d'équivalence.
En pratique
Ceci étant fait on défini le produit par
On vérifie facilement que cette opération est compatible avec la relation
aviateurpilot a écrit:1.(-1)=(-1) car 1 est l'element neutre
merci je sais,
vous ne l'avez pas prouvé pour un nombre négatif. c'est un raisonnement circulaire... vous partez sans connaitre la propriété de 1 element neutre avec les negatifs..
la methode de nuage de reconstruction de Z est plus interessante...
Juste une remarque:
Il ne s'agit pas d'une méthode, mais d'une construction de
Et pas d'une justification, qui peut aider à comprendre, mais d'une démonstration. Et une démonstration peut emporter la conviction, quand on peut la comprendre, mais (en particulier celle là) n'explique rien.
Je suis heureux d'avoir donné une esquisse de démonstration qui emporte ta conviction, mais tu doit bien de rendre compte qu'il s'agit d'une construction >. Les définitions données viennent (au XIX°) pour justifier des règles déjà connues. Et ces règles viennent des arguments heuristiques donnés plus haut.
A+
la methode de nuage de reconstruction de Z est plus interessante...
Il ne s'agit pas d'une méthode, mais d'une construction de
Et pas d'une justification, qui peut aider à comprendre, mais d'une démonstration. Et une démonstration peut emporter la conviction, quand on peut la comprendre, mais (en particulier celle là) n'explique rien.
Je suis heureux d'avoir donné une esquisse de démonstration qui emporte ta conviction, mais tu doit bien de rendre compte qu'il s'agit d'une construction >. Les définitions données viennent (au XIX°) pour justifier des règles déjà connues. Et ces règles viennent des arguments heuristiques donnés plus haut.
A+
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
