slt
voila une petite confusion qui m'a coute cher
1)fonction peut posseder plusieurs points a l'origine :vrai
2)une fonction lineaire ne possede pas d'ordonne a l'origine:faux
je ne comprends pas la 1)...pkoi c'est vrai a moins que se soit faux...
pouvez vous faire un graphique? aussi les minimums absolus est-ce qu'ils faut que la courbe monte toute suite apres? comme les maximums absolus,locaux?
merci
Petite confusion
5 messages
- Page 1 sur 1
Bonjour,
Jen17, en quelle classe es-tu?
Reprends ce que je dis à Mikou. Ainsi, une fonction définie en 0 associe toujours au point d'abscisse 0 l'unique valeur f(0). Autrement dit, pour une fonction définie en 0, il existe toujours une et une seule ordonnée à l'origine.
Quelle est la particularité d'une fonction linéaire? Quelle est donc l'ordonnée à l'origine d'une fonction linéaire?
Je ne vais te répondre que pour les minimums (ou minima - pour qui voudra débattre avec moi sur la question des pluriels des mots latins...) car c'est évidemment analogue pour les maximums.
Rappelons la définition d'un minimum absolu:
Soit une fonction , avec
, avec 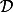 son domaine de définition. Dire que f admet un minimum absolu sur
son domaine de définition. Dire que f admet un minimum absolu sur 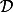 signifie qu'il existe un point
signifie qu'il existe un point  appartenant à
appartenant à 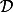 tel que pour tout x appartenant à
tel que pour tout x appartenant à 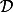 ,
, {\ge}f(x_0)) . Donc "la courbe remonte après
. Donc "la courbe remonte après  " comme tu dis, de même qu'elle descend avant
" comme tu dis, de même qu'elle descend avant  .
.
Attention, le minimum absolu peut être atteint en plusieurs points ,
,  ,..., mais tu auras quand même
,..., mais tu auras quand même =f(x_2)=f(x_0)) . En gros, la courbe descendra vers son minimum, l'atteindra en
. En gros, la courbe descendra vers son minimum, l'atteindra en  , puis remontra et redescendra pour l'atteindre à nouveau en
, puis remontra et redescendra pour l'atteindre à nouveau en  , et ce peut-être pluusieurs fois (en
, et ce peut-être pluusieurs fois (en  ,
, 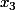 , etc...), mais ne descendra jamais plus bas.
, etc...), mais ne descendra jamais plus bas.
Un cas particulier de cela est si ta fonction est constante là où elle atteint son minimum. Alors elle attendra la fin de ce segment pour remonter! :happy2:
En ce qui concerne les minimums locaux, cela signifie que si on restreint la fonction à un certain intervalle, cette restriction de la fonction admet un minimum global sur cet intervalle. Bon, assez de maths formelles, parlons en français maintenant!
En fait, il faut comprendre que si tu regardes un intervalle inclus dans le domaine de définition de la fonction, et qu'un point est un minimum global sur cet intervalle, alors on dit que f admet un minimum local en ce point (et en précisant l'intervalle).
J'espère t'avoir un peu éclairé(e) sur le sujet car ça avait l'air très confus chez toi, et surtout n'hésite pas à poser des questions!
Bon courage et à bientôt :++: ,
Zeb
Attention!!! On parle ici de fonction. Une fonction associe à chaque point de son domaine de définition un et un seul point!Mikou a écrit:trace un cercle de centre (0;0) et de rayon 1...
jen17 a écrit:1)fonction peut posseder plusieurs points a l'origine :vrai
Jen17, en quelle classe es-tu?
Reprends ce que je dis à Mikou. Ainsi, une fonction définie en 0 associe toujours au point d'abscisse 0 l'unique valeur f(0). Autrement dit, pour une fonction définie en 0, il existe toujours une et une seule ordonnée à l'origine.
Jen17 a écrit:2)une fonction lineaire ne possede pas d'ordonne a l'origine:faux
Quelle est la particularité d'une fonction linéaire? Quelle est donc l'ordonnée à l'origine d'une fonction linéaire?
Jen17 a écrit:les minimums absolus est-ce qu'ils faut que la courbe monte toute suite apres? comme les maximums absolus,locaux?
Je ne vais te répondre que pour les minimums (ou minima - pour qui voudra débattre avec moi sur la question des pluriels des mots latins...) car c'est évidemment analogue pour les maximums.
Rappelons la définition d'un minimum absolu:
Soit une fonction
Attention, le minimum absolu peut être atteint en plusieurs points
Un cas particulier de cela est si ta fonction est constante là où elle atteint son minimum. Alors elle attendra la fin de ce segment pour remonter! :happy2:
En ce qui concerne les minimums locaux, cela signifie que si on restreint la fonction à un certain intervalle, cette restriction de la fonction admet un minimum global sur cet intervalle. Bon, assez de maths formelles, parlons en français maintenant!
En fait, il faut comprendre que si tu regardes un intervalle inclus dans le domaine de définition de la fonction, et qu'un point est un minimum global sur cet intervalle, alors on dit que f admet un minimum local en ce point (et en précisant l'intervalle).
J'espère t'avoir un peu éclairé(e) sur le sujet car ça avait l'air très confus chez toi, et surtout n'hésite pas à poser des questions!
Bon courage et à bientôt :++: ,
Zeb
Attention
Une fonction f d'un ensemble A à un ensemble B, c'est un "truc" qui pour tout x de A associe un UNIQUE y de B :
f : A -> B
f : x |-> y
f : A -> B
f : x |-> y
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
