Nombres de numéros de téléphone...

[abaque75]

Bonjour à tous :lol3:

Complétement néophyte, je ne sais pas trop si je poste au le bon endroit, je voudrais poser une question relative je crois à l'analyse combinatoire :

Combien de numéros de téléphone portable peut-on créer avec la série de 10 chiffres 06 :

06 xx xx xx xx

Quelle est la formule qui permet de trouver ce nombre ?


D' autre part est-il vrai que le nombre d'ordonnancement d'un jeu de 52 cartes est égal au nombre stupéfiant de 8 suivi de 67 numéros !

(Svp soyez simple dans vos réponses je suis nul en math)

Merci d'avance :lol3:

[fatal_error]

salut,

combien tu peux écrire de nombres différents avec x, et xx, et xxx?

pour lordonnancement des 52 cartes, tu écris
xxxxx...xx
(52 x)
le premier x t'as 52 choix, le deuxieme x, 51, le troisieme 50... etc...
ca te fait 52!, jte laisse calculer ca avec ta babasse

[nodjim]

La réponse pour les cartes est exacte, c'est un nombre à 68 chiffres qui commence par 8 et qui finit par 15 zéros.
Si les 6 milliards d'êtres humains d'aujourd'hui avaient commencé à compter ensemble ce nombre, à raison de 1 nombre par seconde chacun, depuis la naissance de l'univers, on serait encore très très loin d'avoir fini de compter....

[abaque75]

La réponse pour les cartes est exacte, c'est un nombre à 68 chiffres qui commence par 8 et qui finit par 15 zéros.
Si les 6 milliards d'êtres humains d'aujourd'hui avaient commencé à compter ensemble ce nombre, à raison de 1 nombre par seconde chacun, depuis la naissance de l'univers, on serait encore très très loin d'avoir fini de compter....

Merci :lol3:

Mais je n'ai pas de réponses pour le pb des numéros de téléphone... :hein:

[pinocchio]

Bonjour,
si des fois tu revenais lire ce sujet :happy2: :

pour les numéros de téléphone,
tu as 10 possibilités pour le premier chiffre, (les chiffres de 0 à 9)
10 possibilités pour le deuxième chiffre,
10 possibilités pour le troisième...
ainsi de suite jusqu'au huitième chiffre.

ça fait
10x10x10x10x10x10x10x10=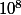= 100 000 000 de possibilités
100 millions de possibilités
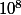(, 10 puissance 8, c'est un 1 avec huit zéros derrière)

si tu es "complètement néophyte" comme tu le dis,
peut-être que tu ne vois pas pourquoi on multiplie le 10 huit fois de suite
enfin, évidemment, huit fois c'est parce qu'il y a huit chiffres dans le numéro, et dix parce qu'il y a dix chiffres de 0 à 9,
mais peut-être que tu ne vois pas pourquoi il faut multiplier.

Alors pour faire plus simple, imagine que tu veuilles savoir combien de numéros de téléphone de trois chiffres tu peux former avec seulement les chiffres 0 et 1
(oui, ça n'a pas de sens , mais ça vaut peut-être le coup de simplifier)

pour le premier chiffre, tu as deux possibilités, puisque tu as le choix entre 0 et 1
pour le deuxième pareil,
pour le troisième pareil.

On peut faire ce qu'on appelle un arbre :
de chacune des branches partent deux autres branches, à chaque nouveau chiffre qu'il faut choisir.

tu vois qu'en suivant la première branche, ça forme le numéro 000
puis 001, 010, 011, 100, 101, 110, 111.
8 "numéros de téléphone" différents,
car tu as 2 possibilités pour le premier chiffre, 2 pour le deuxième, 2 pour le troisième.
2x2x2=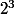=8
On voit sur l'arbre pourquoi il faut multiplier,
car de chacune des branches on fait partir de nouvelles branches

Si tu veux faire un numéro à 12 chiffres avec seulement des 0 et des 1,
il faudra multiplier 2 par lui-même 12 fois, 2 puissance 12, .
Si tu veux faire des numéros de 12 chiffres composés avec les chiffres de 0 à 9 comme dans ton exemple, il faudra multiplier 10 par lui-même 12 fois au lieu de 8 comme dans ton exemple,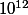
(ça fera un 1 avec 12 zéros, 1000 milliards de numéros de téléphone différents).

Tu peux essayer de faire des arbres simples pour comprendre le principe,
(car avec trop de possibilités, on ne peut plus dessiner toutes les branches, c'est juste pour comprendre le principe)
par exemple, combien tu peux former de numéros différents de 3 chiffres avec les chiffres 1,2 et 3.

Comme te l'a expliqué Fatal Error plus haut,
le problème des 52 cartes est un peu différent puisque quand tu choisis une carte à mettre en premier,
tu ne la remets pas ensuite dans le jeu et tu ne peux pas la piocher à nouveau,
il faut donc l'enlever du choix et ne plus la compter,
c'est pourquoi pour la première carte tu as 52 possibilités, 51 possibilités pour la deuxième carte, 50 possibilités pour la troisième carte...

[abaque75]

Bonjour,
si des fois tu revenais lire ce sujet :happy2: :

pour les numéros de téléphone,
tu as 10 possibilités pour le premier chiffre, (les chiffres de 0 à 9)
10 possibilités pour le deuxième chiffre,
10 possibilités pour le troisième...
ainsi de suite jusqu'au huitième chiffre.

ça fait
10x10x10x10x10x10x10x10== 100 000 000 de possibilités
100 millions de possibilités
(, 10 puissance 8, c'est un 1 avec huit zéros derrière)

si tu es "complètement néophyte" comme tu le dis,
peut-être que tu ne vois pas pourquoi on multiplie le 10 huit fois de suite
enfin, évidemment, huit fois c'est parce qu'il y a huit chiffres dans le numéro, et dix parce qu'il y a dix chiffres de 0 à 9,
mais peut-être que tu ne vois pas pourquoi il faut multiplier.

Alors pour faire plus simple, imagine que tu veuilles savoir combien de numéros de téléphone de trois chiffres tu peux former avec seulement les chiffres 0 et 1
(oui, ça n'a pas de sens , mais ça vaut peut-être le coup de simplifier)

pour le premier chiffre, tu as deux possibilités, puisque tu as le choix entre 0 et 1
pour le deuxième pareil,
pour le troisième pareil.

On peut faire ce qu'on appelle un arbre :
de chacune des branches partent deux autres branches, à chaque nouveau chiffre qu'il faut choisir.

tu vois qu'en suivant la première branche, ça forme le numéro 000
puis 001, 010, 011, 100, 101, 110, 111.
8 "numéros de téléphone" différents,
car tu as 2 possibilités pour le premier chiffre, 2 pour le deuxième, 2 pour le troisième.
2x2x2==8
On voit sur l'arbre pourquoi il faut multiplier,
car de chacune des branches on fait partir de nouvelles branches

Si tu veux faire un numéro à 12 chiffres avec seulement des 0 et des 1,
il faudra multiplier 2 par lui-même 12 fois, 2 puissance 12, .
Si tu veux faire des numéros de 12 chiffres composés avec les chiffres de 0 à 9 comme dans ton exemple, il faudra multiplier 10 par lui-même 12 fois au lieu de 8 comme dans ton exemple,
(ça fera un 1 avec 12 zéros, 1000 milliards de numéros de téléphone différents).

Tu peux essayer de faire des arbres simples pour comprendre le principe,
(car avec trop de possibilités, on ne peut plus dessiner toutes les branches, c'est juste pour comprendre le principe)
par exemple, combien tu peux former de numéros différents de 3 chiffres avec les chiffres 1,2 et 3.

Comme te l'a expliqué Fatal Error plus haut,
le problème des 52 cartes est un peu différent puisque quand tu choisis une carte à mettre en premier,
tu ne la remets pas ensuite dans le jeu et tu ne peux pas la piocher à nouveau,
il faut donc l'enlever du choix et ne plus la compter,
c'est pourquoi pour la première carte tu as 52 possibilités, 51 possibilités pour la deuxième carte, 50 possibilités pour la troisième carte...

Un grand merci Pinocchio pour ces explications simples et faciles à comprendre :lol3:

[ksavier]

roooooo,

Je ne vois pas d'arbre ici, ni de calcul compliqué

Il suffit de les écrire tous (sans le 06 qui est imposé) !!

00 00 00 00
00 00 00 01
00 00 00 02
00 00 00 03
...
00 00 00 99
00 00 01 00
00 00 01 01
00 00 01 02
...

Bref, on compte quoi ! à chaque entier correspond un numéro et inversement chaque numéro correspond un entier

Le dernier est 99 99 99 99

Il y a 100 000 000 de nombres entiers compris entre 0 et 99 999 999.
autant de numéros de téléphone.

[ksavier]

En ce qui concerne la seconde question,

52 cartes.

Pour la première carte il y a 52 cartes possibles;
Pour chaque première carte, il y a 51 cartes possibles pour la deuxième.

Pour l'instant il y a 52x51=2 652 possibilités

Pour chacune de ces possibilités il y a 50 cartes possibles.

Ainsi il y a 52x51x50= 132 600 possibilités d'ordonner 3 cartes.

Etc.

Il y a 52x51x50x49x48x...x3x2x1 = 80 658 175 170 943 878 571 660 636 856 403 766 975 289 505 440 883 277 824 000 000 000 000 possibilités d'ordonner 52 cartes.

Exact, cela fait bien un 8 et 67 numéros.

[pinocchio]

Ah oui, Ksavier, ton explication est encore plus simple. :lol4:

Et effectivement, il n'y a pas besoin d'arbre : moi j'ai toujours tendance à faire des arbres à cause des probabilités, mais là c'est de la combinatoire...

Sinon pour calculer 52x51x50x49x48x...x3x2x1 = 80 658 175 170 943 878 571 660 636 856 403 766 975 289 505 440 883 277,

on peut aussi préciser à Abaque 75,
-s'il n'a pas appris les factorielles-

en raccourci, (52x51x50x49x48x...x3x2x1)

ça se note 52!, (comme le mettait Fatal Error plus haut)

52 avec un point d'exclamation après,
ça veut dire que c'est la multiplication entre eux de tous les chiffres entre 52 et 1, et ça s'appelle la factorielle de 52.

Sur une calculatrice scientifique, il y a souvent une touche avec un point d'exclamation pour calculer les factorielles,
ce qui évite de taper 51 multiplications d'affilée :dingue:
il suffit de taper 52 puis la touche factorielle

mais pour 52!, comme c'est un nombre à 68 chiffres, la calculette abrège un peu...

Par exemple, si tu tapes "52!" dans la barre de recherche de Google, ça donne ce résultat,
qui est le même résultat (arrondi) que te donne Ksavier (en "notation scientifique", 8.06581752 multiplié par 10 puissance 67)

Par exemple, si tu tapes 5!, une calculette (ou Google) te donne 120,
et tu trouves la même chose en calculant (5x4x3x2x1).

[abaque75]

Ah oui, Ksavier, ton explication est encore plus simple. :lol4:

Et effectivement, il n'y a pas besoin d'arbre : moi j'ai toujours tendance à faire des arbres à cause des probabilités, mais là c'est de la combinatoire...

Sinon pour calculer 52x51x50x49x48x...x3x2x1 = 80 658 175 170 943 878 571 660 636 856 403 766 975 289 505 440 883 277,

on peut aussi préciser à Abaque 75,
-s'il n'a pas appris les factorielles-

en raccourci, (52x51x50x49x48x...x3x2x1)

ça se note 52!, (comme le mettait Fatal Error plus haut)

52 avec un point d'exclamation après,
ça veut dire que c'est la multiplication entre eux de tous les chiffres entre 52 et 1, et ça s'appelle la factorielle de 52.

Sur une calculatrice scientifique, il y a souvent une touche avec un point d'exclamation pour calculer les factorielles,
ce qui évite de taper 51 multiplications d'affilée :dingue:
il suffit de taper 52 puis la touche factorielle

mais pour 52!, comme c'est un nombre à 68 chiffres, la calculette abrège un peu...

Par exemple, si tu tapes "52!" dans la barre de recherche de Google, ça donne ce résultat,
qui est le même résultat (arrondi) que te donne Ksavier (en "notation scientifique", 8.06581752 multiplié par 10 puissance 67)

Par exemple, si tu tapes 5!, une calculette (ou Google) te donne 120,
et tu trouves la même chose en calculant (5x4x3x2x1).

Merci à tous :lol3:

J'en reviens aux n° de téléphone....

==> Alors aux USA ils sont plus de 300 millions ! Comment font-ils ?

10 chiffres ==> maxi 100 millions

Ils ont des numeros à 12 chiffres ou plus ? :hein:


Au fait la solution "10 puissance 8" pour les numéros de téléphone c'est de l'arrangement, de la permutation ou de la combinaison ? :hein:

[pinocchio]

Bonsoir,
si j'en crois ce document , le nombre de numéros de téléphone c'est un arrangement avec répétition :
"une collection de 8 objets pris successivement parmi 10 en tenant compte de l'ordre d'apparition", et comme on peut mettre un chiffre plusieurs fois dans le même numéro, c'est un arrangement avec répétition.

Alors que ton autre question, de combien de façons différentes on peut ranger un jeu de 52 cartes, c'est un problème de permutation simple (sans répétition) : on tient compte de l'ordre des cartes.

Les combinaisons, ça ne tient pas compte de l'ordre : le loto, par exemple, ne tient pas compte de l'ordre dans lequel les numéros sont tirés, donc quand on cherche combien il y a de façons de tirer les boules au loto, on cherche le nombre de combinaisons.
(par exemple au loto, 6-12-23-45-3, c'est la même chose que 12-3-23-6-45, donc il faut enlever tous ces "doublons" quand on cherche le nombre de combinaisons)

[pinocchio]

==> Alors aux USA ils sont plus de 300 millions ! Comment font-ils ?

10 chiffres ==> maxi 100 millions

Ils ont des numeros à 12 chiffres ou plus ? :hein:

En fait, un numéro de 10 chiffres, ça fait : arrangements,
c'est-à-dire un 1 avec 10 zéros derrière : 10 000 000 000
10 milliards de numéros.

100 millions, c'est pour un numéro de 8 chiffres, (parce que dans ta question du début, tu demandais un numéro commençant en 06 avec 8 chiffres derrière, le 06 étant imposé)

Si j'en crois ce lien , les numéros américains, (je ne comprends pas bien si ce sont les fixes ou les mobiles ou bien les deux ??) ont une dizaine de chiffres (un indicatif de zone de 3 chiffres, et un numéro de 7 chiffres).

[pinocchio]

Bon, je n'ai pas trouvé de document plus clair sur les numéros américains, mais un exercice (page 8 du PDF) qui dit :

"Il y a 680 numéros à 3 chiffres utilisables comme indicatif de zones en Amérique du Nord.
En Avril 2002, seulement 305 d'entre eux étaient vraiment utilisés..."

Comme les numéros ont 7 chiffres si on met de côté les 3 chiffres de l'indicatif, ça fait 10 puissance 7 : 10 millions de numéros par zone.
680 indicatifs de zones multiplié par 10 millions, il y a encore de quoi faire, ça fait 6,8 milliards de numéros en tout.

[abaque75]

Bon, je n'ai pas trouvé de document plus clair sur les numéros américains, mais un exercice (page 8 du PDF) qui dit :

"Il y a 680 numéros à 3 chiffres utilisables comme indicatif de zones en Amérique du Nord.
En Avril 2002, seulement 305 d'entre eux étaient vraiment utilisés..."

Comme les numéros ont 7 chiffres si on met de côté les 3 chiffres de l'indicatif, ça fait 10 puissance 7 : 10 millions de numéros par zone.
680 indicatifs de zones multiplié par 10 millions, il y a encore de quoi faire, ça fait 6,8 milliards de numéros en tout.

Merci Pinocchio :lol3:
Toujours aussi clair et réactif.

[emiliey]

Merci Pinocchio :lol3:
Toujours aussi clair et réactif.

Bonjour,

Je vous écris par ici car je ne sais pas comment ouvrir une discussion -.-' je suis nouvelle sur ce site..
Le problème que j'ai c'est que j'ai un DM de math (je suis en 1ère ES) et il y a un exercice sur les suites que je n'arrive pas à le faire entièrement :/ à partir de la question 3 je bloque.. donc j'aimerai bien avoir un peu d'aide de votre part Svp :$

Voici l'exercice:

on considère la suite Un pour tout n appartenant à N : U0= 2 et Un+1= 2/3Un+1 , pour n appartient à N

1) Calculer u1, u2, u3

2) la suite (Un) est-elle arithmétique ? géométrique?

(a partir de là je n'y arrive plus .. )

3) on définit la suite (Vn) par Vn=Un-3 pour tout n appartient à N

a. calculer V0, V1, V2
b. Déterminer la nature de la suite (Vn)
c. En déduire l'expression de Vn en fonction de n

4) a.Exprimer Un en fonction de Vn, puis en fonction de n
b. Calculer U8

Aidez moi svp :'(

Je vous remercie d'avance, en attendant une réponse assez rapidement de votre part!

Emilie.Y

[sad13]

salut @ tous; merci Pinnochio, j'avais bien compris au début avec les arbres et 10^10 mais à la fin vous parlez d'arrangements et je ne comprends plus.

Dans le 10^10, on n'inclut pas le cas "où les 10 chiffres sont égaux? "
je dirais oui, à voir l'arbre où l'on a 000 ou 111 ........

[Dlzlogic]

salut @ tous; merci Pinnochio, j'avais bien compris au début avec les arbres et 10^10 mais à la fin vous parlez d'arrangements et je ne comprends plus.

Dans le 10^10, on n'inclut pas le cas "où les 10 chiffres sont égaux? "
je dirais oui, à voir l'arbre où l'on a 000 ou 111 ........

Bonjour,
C'est effectivement l'arrangement de 10 chiffres (0 à 9) 10 à 10 (les 10 chiffres d'un numéro).
Mais il me parait beaucoup plus simple de raisonner en disant "il y a C caractères différents et n positions" alors le nombres de possibilités est C^n.
Application nouveau numéro minéralogique : 2 lettres 3 chiffres 2 lettres
26^2 * 10^3 * 26^2
Il y a juste un petit doute sur le 10^3, je ne sais pas si "000" est possible, ou "001" ?
Autre application, avec les 10 doigts, on peut compter jusqu'à 1024-1

[sad13]

10^10 c'est faux pour les nums de téléphones car l'arbre dessiné reflète bien le problème et je ne vois pas pourquoi ça serai Arrangement de 10 parmi 10?

Ben avec les 10 doigts , on peut compter de 1 à10; puis 20 ou 25 etc je ne comprends pas pourquoi spécialement 1024-1

[Dlzlogic]

10^10 c'est faux pour les nums de téléphones car l'arbre dessiné reflète bien le problème et je ne vois pas pourquoi ça serai Arrangement de 10 parmi 10?

Ben avec les 10 doigts , on peut compter de 1 à10; puis 20 ou 25 etc je ne comprends pas pourquoi spécialement 1024-1

Bonjour,
Voir ce sujet
http://www.maths-forum.com/showthread.php?t=122703&highlight=1024
Et il y en a d'autres.

[sad13]

merci mais Pinnochio lui même a dit que c'est 10^3;, bref les probas c'est pas pr moi