Je développe, à mon rythme… une application de PathFinding reprenant le principe de Dijkstra. Je n’ai de cesse de l’améliorer voilà pourquoi ce sujet.
Mon PathFinder s’applique à des matrices sur Excel qui peuvent être à 2 ou 3 dimensions et prévoit deux modes de cheminement distincts : adjacent (4 carrés partageant une arête avec un carré central en 2D ; 6 cubes partageant une face en 3D) ou périphérique (8 carrés voisins d’un carré central en 2D ; 26 cubes autour en 3D).
Je souhaiterais ici étudier le cas des matrices 2D avec cheminement adjacent et pondérées de façon totalement aléatoire. Si j’obtiens réponse peut-être sera-t-il simple d’étendre le principe aux autres modes ?
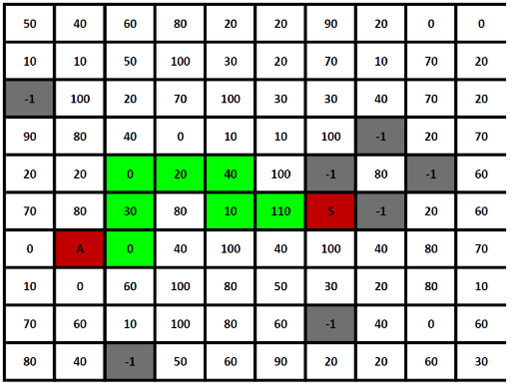
Trois grandeurs liées à chacun des carrés sont actuellement considérées dans cet algo :
- L’IC : Individual Cost ; les valeurs que l’on retrouve sur la feuille Excel.
- Le TC : Total Cost ; l’addition des coûts rencontrés depuis le point de départ jusqu’à un carré en empruntant le plus court-chemin. Une sorte de distance pondérée.
- Le Path : est une info de type (x, y) avec x et y pouvant être -1, 0 ou 1 servant à remonter le chemin depuis un carré jusqu’au point de départ et permettant de tracer ce chemin.
Actuellement mon algo calcule les carrés concentriquement au point de départ jusqu’à ce que l’arrivée soit trouvée, le résultat renvoyé et le calcul interrompu. Du moins dans le cas où la matrice n’est pas pondérée, les pondérations faussent un peu la donne.
Le problème peut peut-être se poser de la sorte ? :
Imaginons que nous partons de Paris, que nous allons à Clermont-Ferrand et avons réussi à nous en approcher beaucoup, est-il encore utile de s’intéresser à ce qui se passe vers Lille ?
Donc mon idée serait d’introduire pour chacun des carrés une quatrième grandeur la DANP ou Distance à l’Arrivée Non Pondérée, soit le nombre de cases séparant un carré de l’arrivée, calcul simple et rapide à effectuer ; et introduire dans l’algo une variable (une pour tout l’algo et non pas pour chacun des carrés) qui pourrait s’appeler Nearest et qui enregistrerait à quelle distance (en nombre de cases) le carré calculé le plus proche du point d’arrivée se trouve.
On aurait alors affaire à une comparaison de deux groupes partageant un même random mais de quantité différente :
Si par exemple mon Nearest est de 3 et qu’un carré se situe à une distance DANP de 15 quelle probabilité y a-t-il que la somme de ces 15 unités aléatoires soit strictement inférieure à la somme des 3 unités du Nearest ? Si la probabilité est vraiment très faible on peut alors avec peu de risque raturer ce carré et l’exclure du processus glouton. En plus de cet aspect les TC de ce carré et du carré correspondant au Nearest ont naturellement aussi une incidence sur cette probabilité ce qui finit de rendre le problème intéressant.
Si le principe est OK ( ?) au niveau de la quantification je bute. Certainement les paramètres suivants sont à prendre en compte :
- La nature du random (étendue, nombre de valeurs distinctes ?)
- L’acceptation ou non du zéro (mon algo doit l’accepter)
- Les TC des carrés
- Les DANP des carrés
- Le Nearest
- Autres ?
Voilà maintenant le problème posé, merci à celles ou ceux qui souhaiterons m’aider (en validant ou non le principe exposé ici puis sur sa quantification si le principe est validé). Malheureusement mon niveau en Maths est bas et m’empêche de comprendre certaines écritures mathématiques, ne vous étonnez donc pas si je serais amené à poser des questions qui peuvent vous sembler évidentes.
Et en accord avec la charte du forum me donner des pistes me permettant d’avancer me plairait beaucoup plus qu’une solution toute trouvée !
Merci d’avance
PS : Moins en accord avec la charte ce sujet est une réédition d’un sujet ancien à peine différent malencontreusement placé dans la rubrique : « Lycée » qui ne m’avait permis d’avancer que partiellement.
