Intégrale indéfinie / primitive
Discussion générale entre passionnés et amateurs de mathématiques sur des sujets mathématiques variés
-
Cryptocatron-11
- Membre Rationnel
- Messages: 604
- Enregistré le: 18 Déc 2010, 20:19
-
 par Cryptocatron-11 » 19 Sep 2012, 05:30
par Cryptocatron-11 » 19 Sep 2012, 05:30
Bonjour,
J'aimerais savoir s'il est correcte en maths d'écrire
 dt = F(t))
? Si oui, comment s'appelle F(t) ? est ce une intégrale indéfinie ou une primitive ? J'avoue que je ne distingue pas bien la différence entre intégrale indéfinie et primitive...
Je vois souvent cette écriture
 = \int_{a}^{x} f(t) dt = F(x) - F(a) = F(x))
avec F une fonction qui s'annule en a.
Dans ce cas mon F(t) et mon F(x) ne signifie pas la même chose. F(t) est une fonction alors que F(x) est une valeur numérique.
Merci de m'éclairer un peu même si la question paraît un peu bête (elle me turlupine depuis longtemps). Y'aurait pas un peu d'algèbre au niveau de l'écriture derrière tout ça ?
-
Anonyme
 par Anonyme » 19 Sep 2012, 07:48
par Anonyme » 19 Sep 2012, 07:48
 dt)
est la limite de F(x) quand x tend vers +infini
et cette intégrale est définie si cette limite est finie
F étant une primitive de f
Remarque :
Souvent on n'a pas besoin de calculer F pour démontrer qu'une telle intégrale est définie
-
Cryptocatron-11
- Membre Rationnel
- Messages: 604
- Enregistré le: 18 Déc 2010, 20:19
-
 par Cryptocatron-11 » 19 Sep 2012, 08:02
par Cryptocatron-11 » 19 Sep 2012, 08:02
D'accord. Mais tu n'as pas répondu à ma première question.
-
Anonyme
 par Anonyme » 19 Sep 2012, 08:16
par Anonyme » 19 Sep 2012, 08:16
La relation intégrale et primitive est celle que tu as écrit dans ton premier message
 dt)
est LA primitive de la fonction f qui s'annule en a
Une intégrale indéfinie n'est pas une primitive ( tu vois bien que cela revient à un cacul de limite)
Une primitive est une fonction et non pas un nombre
 dt)
est un nombre qu'on peut également souvent calculer par F(b)-F(a) si F existe
-
Cryptocatron-11
- Membre Rationnel
- Messages: 604
- Enregistré le: 18 Déc 2010, 20:19
-
 par Cryptocatron-11 » 19 Sep 2012, 08:22
par Cryptocatron-11 » 19 Sep 2012, 08:22
ptitnoir a écrit: dt)
est LA primitive de la fonction f qui s'annule en a
 dt)
qui est égal à F(x) n'est pas une primitive c'est une valeur numérique...
-
Anonyme
 par Anonyme » 19 Sep 2012, 08:24
par Anonyme » 19 Sep 2012, 08:24
NON c'est une fonction de la variable x
-
Cryptocatron-11
- Membre Rationnel
- Messages: 604
- Enregistré le: 18 Déc 2010, 20:19
-
 par Cryptocatron-11 » 19 Sep 2012, 08:26
par Cryptocatron-11 » 19 Sep 2012, 08:26
Dire que F(x) est une fonction ça me parait :doh: . Dire que F est une fonction OK mais F(x) ça reste une valeur numérique , non ?
-
Anonyme
 par Anonyme » 19 Sep 2012, 08:26
par Anonyme » 19 Sep 2012, 08:26
De plus
 dt =F(x) - F(a)=G(x)-G(a))
avec F et G deux primitives de le fonction f
-
Anonyme
 par Anonyme » 19 Sep 2012, 08:27
par Anonyme » 19 Sep 2012, 08:27
Cryptocatron-11 a écrit:Dire que F(x) est une fonction ça me parait :doh: . Dire que F est une fonction OK mais F(x) ça reste une valeur numérique , non ?
Tu as raison c'est un abus de langage car on devrait dire la fonction F définie par F(x)=....
ps) où as tu lu que j'ai écrit F(X) est une fonction ?
-
Cryptocatron-11
- Membre Rationnel
- Messages: 604
- Enregistré le: 18 Déc 2010, 20:19
-
 par Cryptocatron-11 » 19 Sep 2012, 08:38
par Cryptocatron-11 » 19 Sep 2012, 08:38
ptitnoir a écrit:on devrait dire la fonction F définie par F(x)=....
Là je préfère :lol3:
ptitnoir a écrit:où as tu lu que j'ai écrit F(X) est une fonction ?
Tu n'as pas vraiment dit ça, tu as dit :
 dt)
est LA primitive de la fonction f qui s'annule en a.
Mais ça revient au même car
 dt)
est aussi une valeur numérique .
-
Cryptocatron-11
- Membre Rationnel
- Messages: 604
- Enregistré le: 18 Déc 2010, 20:19
-
 par Cryptocatron-11 » 19 Sep 2012, 08:42
par Cryptocatron-11 » 19 Sep 2012, 08:42
Bon, je ne sais toujours pas s'il est correcte (en maths) d'écrire
 dt = F(t))
-
Anonyme
 par Anonyme » 19 Sep 2012, 08:43
par Anonyme » 19 Sep 2012, 08:43
 dt=F(x)-F(a))
est bien une valeur numérique qui permet de définir une fonction
On n'a pas
 dt=F(x))
ou
 dt = F(t))
-
Cryptocatron-11
- Membre Rationnel
- Messages: 604
- Enregistré le: 18 Déc 2010, 20:19
-
 par Cryptocatron-11 » 19 Sep 2012, 08:52
par Cryptocatron-11 » 19 Sep 2012, 08:52
Ben si , si F(a) = 0 on a bien
 dt=F(x))
.
ptitnoir a écrit: On n'a pas
 dt = F(t))
Si je pose la question, c'est parce que je l'ai vu écrite dans des cours (de profs apparement certifiés)
Je pensais par exemple à
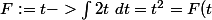)
. Pourquoi on aurait pas le droit d'écrire ça ?
-
Anonyme
 par Anonyme » 19 Sep 2012, 09:05
par Anonyme » 19 Sep 2012, 09:05
Cela n'a aucun sens car si on ne connait pas les bornes d'une intégrale on ne peux rien écrire ou déduire....
Exemples
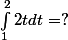
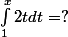
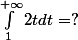
Si tu n'es toujours pas persuadé , je suis désolé de ne pas avoir pu me faire comprendre...
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 19 Sep 2012, 09:30
par Nightmare » 19 Sep 2012, 09:30
Salut,
l'intégrale indéfinie est une notation abusive utilisée pour désigner une primitive quelconque de l'intégrande. Elle est a proscrire des copies autant que possible car peut être source de nombreuses erreurs, notamment sur l'ajout intempestif des constantes additives d'intégration.
-
Anonyme
 par Anonyme » 19 Sep 2012, 09:34
par Anonyme » 19 Sep 2012, 09:34
Cryptocatron-11 a écrit:Je vois souvent cette écriture
 = \int_{a}^{x} f(t) dt = F(x) - F(a) = F(x))
avec F une fonction qui s'annule en a.
Je crois que je viens de comprendre ton problème...
Tu confonds F(a)=0 et la phrase "La primitive qui s'annule en a"
Explications:
Supposons que F et G sont 2 primitives différentes de f
et que
 \ne 0)
et
 \ne 0)
 dt = F(x) - F(a) = G(x)-G(a))
est LA primitive de la fonction f qui s'annule en a
En effet c'est la fonction H définie par
= F(x) - F(a))
qui vérifie H(a)=0
H est donc LA primitive de la fonction f qui s'annule en a
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 19 Sep 2012, 11:47
par Luc » 19 Sep 2012, 11:47
Cryptocatron-11 a écrit:Bon, je ne sais toujours pas s'il est correcte (en maths) d'écrire
 dt = F(t))
Salut!
Je me permets de poster un lien qui devrait t'intéresser.
http://www.maths-forum.com/showthread.php?t=129197&highlight=int%E9graleCe que je peux dire à ce sujet, c'est : comment définirais-tu F?
Rigoureusement, on peut introduire une relation d'équivalence sur l'ensemble des fonctions de [a,b] dans R qui dit fRg ssi il existe une constante C telle que pour tout x de [a,b], f(x)-g(x)=c.
La notation
 dt)
, sans bornes, désignerait alors la classe d'équivalence pour R d'une primitive quelconque de f.
-
Cryptocatron-11
- Membre Rationnel
- Messages: 604
- Enregistré le: 18 Déc 2010, 20:19
-
 par Cryptocatron-11 » 19 Sep 2012, 18:00
par Cryptocatron-11 » 19 Sep 2012, 18:00
Luc a écrit:Ce que je peux dire à ce sujet, c'est : comment définirais-tu F?
Comme ça par exemple :
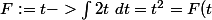)
. Après, si on veut l'évaluer sur un segment [a,b] , on a qu'à écrire
]^{a}_{b} = F(b) - F(a))
. Maintenant reste à savoir qui est " t " ...
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 19 Sep 2012, 18:27
par Luc » 19 Sep 2012, 18:27
Cryptocatron-11 a écrit:Comme ça par exemple :
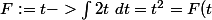)
. Après, si on veut l'évaluer sur un segment [a,b] , on a qu'à écrire
]^{a}_{b} = F(b) - F(a))
. Maintenant reste à savoir qui est " t " ...
Et pourquoi choisis-tu t-> t^2 plutôt que t -> t^2 +1 ou t -> t^2 +18?
-
Cryptocatron-11
- Membre Rationnel
- Messages: 604
- Enregistré le: 18 Déc 2010, 20:19
-
 par Cryptocatron-11 » 19 Sep 2012, 20:49
par Cryptocatron-11 » 19 Sep 2012, 20:49
Luc a écrit:Et pourquoi choisis-tu t-> t^2 plutôt que t -> t^2 +1 ou t -> t^2 +18?
Parce-que quand j'intègrerai, ça reviendra au même . Mais c'est une bonne question, dois je en deduire qqchose ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
