Formule pour densité de plantation
16 messages
- Page 1 sur 1
formule pour densité de plantation
Bonjour à tous,
je trouve de nombreuses sources en ligne pour calculer les densités de plantation.
Malheureusement nul part une formule en fonction du diamètre des plantes.
Par exemple :
sur une surface de 10 m × 10 m,
je vais mettre des plantes qui font 1 m de diamètre,
je veux un espace de passage de 1 m entre chaque plant.
Combien de plants si je plante en alignement carré, et combien en quinconce ?
bien sûr, le calcul de mon exemple est facile à faire.
pour 10x10 si j'ai des plants de 1 m de diamètre et si je veux un passage de 1 m entre chacun, j'ai 25 plants,
si je veux un passage de 2 m j'ai 16 plants, etc.
Ce que je cherche c'est une formule dans laquelle on change un paramètre ou plusieurs pour avoir le résultat du nombre de plants.
j'ai pensé à
(longueur / (diamètre + distance / 2)) x (largeur / (diamètre + distance / 2))
mais ça tombe pas juste
Merci à tous de vos réponses
je trouve de nombreuses sources en ligne pour calculer les densités de plantation.
Malheureusement nul part une formule en fonction du diamètre des plantes.
Par exemple :
sur une surface de 10 m × 10 m,
je vais mettre des plantes qui font 1 m de diamètre,
je veux un espace de passage de 1 m entre chaque plant.
Combien de plants si je plante en alignement carré, et combien en quinconce ?
bien sûr, le calcul de mon exemple est facile à faire.
pour 10x10 si j'ai des plants de 1 m de diamètre et si je veux un passage de 1 m entre chacun, j'ai 25 plants,
si je veux un passage de 2 m j'ai 16 plants, etc.
Ce que je cherche c'est une formule dans laquelle on change un paramètre ou plusieurs pour avoir le résultat du nombre de plants.
j'ai pensé à
(longueur / (diamètre + distance / 2)) x (largeur / (diamètre + distance / 2))
mais ça tombe pas juste
Merci à tous de vos réponses
Re: formule pour densité de plantation
Salut,
Si c'est le diamètre d'un plan et
c'est le diamètre d'un plan et  l'écart que tu veut qu'il y ait entre deux plan alors :
l'écart que tu veut qu'il y ait entre deux plan alors :
- Une "rangée" de 1 plan demande une longueur de .
.
- Une rangée de 2 plans demande une longueur de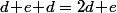 .
.
- Une rangée de 3 plans demande une longueur de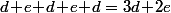 .
.
. . .
- Une rangée de plans demande une longueur de
plans demande une longueur de e=n(d\!+\!e)\!-\!e) .
.
Donc si tu dispose d'une longueur , pour pouvoir y planter une rangée de
, pour pouvoir y planter une rangée de  plans, il faut que
plans, il faut que \!-\!e\!\leq\!\ell) , c'est à dire que
, c'est à dire que 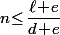 .
.
Et le plus grand entier ayant cette propriété, c'est la partie entière de
ayant cette propriété, c'est la partie entière de 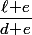 qu'on note
qu'on note ) .
.
Idem dans le sens de la largeur qui, si elle vaut permet de planter au max
permet de planter au max ) plants ce qui fait un total de
plants ce qui fait un total de \!\times\!E\Big(\dfrac{\ell\!+\!e}{d\!+\!e}\Big)) plants (avec une répartition "en carré").
plants (avec une répartition "en carré").
On peut te trouver de même le nombre max que tu en mettra "en quinconce" : le calcul est un peu plus compliqué et risque de contenir deux cas de figure (selon que toutes les rangées ont le même nombre de plant ou que c'est un truc style 5 / 4 / 5 / 4 ....) mais c'est pas la mer à boire.
Si
- Une "rangée" de 1 plan demande une longueur de
- Une rangée de 2 plans demande une longueur de
- Une rangée de 3 plans demande une longueur de
. . .
- Une rangée de
Donc si tu dispose d'une longueur
Et le plus grand entier
Idem dans le sens de la largeur qui, si elle vaut
On peut te trouver de même le nombre max que tu en mettra "en quinconce" : le calcul est un peu plus compliqué et risque de contenir deux cas de figure (selon que toutes les rangées ont le même nombre de plant ou que c'est un truc style 5 / 4 / 5 / 4 ....) mais c'est pas la mer à boire.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: formule pour densité de plantation
Merci pour la réponse rapide,
j'ai essayer de placer cette formule dans un tableur odt, ça donne 144 !
je pense que j'ai pas compris un truc quelque part
j'ai fait une copie d'écran avec la formule développée en dessous du premier tableau
http://image.noelshack.com/fichiers/2018/37/4/1536826909-20.png

j'ai essayer de placer cette formule dans un tableur odt, ça donne 144 !

je pense que j'ai pas compris un truc quelque part

j'ai fait une copie d'écran avec la formule développée en dessous du premier tableau
http://image.noelshack.com/fichiers/2018/37/4/1536826909-20.png

Re: formule pour densité de plantation
Pour interpréter une formule mathématique avec + , - , * , / , un tableur (ou tout autre appareil électronique ou tout mathématicien) utilise ce qu'on appelle "les règles de priorité des opérateurs" :
(1) Les multiplications et divisions sont prioritaires sur les additions et soustractions :
3x7-7 signifie (3x7)-5 et pas 3x(7-5)
3+5/7 signifie 3+(5/7) et pas (3+5)/7
(2) Les opérations de même priorité sont effectuées de gauche à droite :
10 - 5 + 3 signifie (10 - 5) + 3 et pas 10 - (5 + 3)
10/5*3 signifie (10/5)*3 et pas 10/(5*3)
Bref, ta case avec $L$1 + B$8/$D$1 + B$8 elle signifie $L$1 + (B$8/$D$1) + B$8 alors que la formule que je t'ai donné, c'est ($L$1+B$8) / ($D$1+B$8 ).
De plus, il te manque les parties entières. Avec LibreOffice, une des fonction donnant la partie entière est ENT() donc le contenu de ta case, ça doit être :
ENT( ($L$1+B$8) / ($D$1+B$8 ) ) * ENT( ($L$2+A$7) / ($D$1+A$7 ) )
(modulo que les cases L1, B8, etc contiennent bien les bonnes valeurs)
(1) Les multiplications et divisions sont prioritaires sur les additions et soustractions :
3x7-7 signifie (3x7)-5 et pas 3x(7-5)
3+5/7 signifie 3+(5/7) et pas (3+5)/7
(2) Les opérations de même priorité sont effectuées de gauche à droite :
10 - 5 + 3 signifie (10 - 5) + 3 et pas 10 - (5 + 3)
10/5*3 signifie (10/5)*3 et pas 10/(5*3)
Bref, ta case avec $L$1 + B$8/$D$1 + B$8 elle signifie $L$1 + (B$8/$D$1) + B$8 alors que la formule que je t'ai donné, c'est ($L$1+B$8) / ($D$1+B$8 ).
De plus, il te manque les parties entières. Avec LibreOffice, une des fonction donnant la partie entière est ENT() donc le contenu de ta case, ça doit être :
ENT( ($L$1+B$8) / ($D$1+B$8 ) ) * ENT( ($L$2+A$7) / ($D$1+A$7 ) )
(modulo que les cases L1, B8, etc contiennent bien les bonnes valeurs)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: formule pour densité de plantation
oui, bien sûr, les priorités, ça remonte à bien loin tout ça 
sinon c'est super ça marche bien !
http://image.noelshack.com/fichiers/2018/37/4/1536861674-20.png

pour les quinconces :
pourquoi j'ai un affichage d'erreur dans J6 ?
est-ce que ma formule est bonne pour le calcule de distance entre rang (hauteur du triangle) ? ça me semble bien compliqué comme formule, j'ai trouvé ça sur un blog d'assistance scolaire.
la formule est en dessous du tableau
Passez une très bonne soirée
sinon c'est super ça marche bien !
http://image.noelshack.com/fichiers/2018/37/4/1536861674-20.png

pour les quinconces :
pourquoi j'ai un affichage d'erreur dans J6 ?
est-ce que ma formule est bonne pour le calcule de distance entre rang (hauteur du triangle) ? ça me semble bien compliqué comme formule, j'ai trouvé ça sur un blog d'assistance scolaire.
la formule est en dessous du tableau
Passez une très bonne soirée
Re: formule pour densité de plantation
Concernant l'erreur, je sais pas trop et sans avoir accès au fichier (ce qui permet de tester la formule "petit bout par petit bout"), c'est plus que très chiant de repérer où est l'erreur.
Par contre, juste en la regardant "en diagonale", je comprend pas bien ce qu'elle est sensée calculer la formule en question vu que je vois pas trop quelle utilité pourrait avoir une racine d'un gros truc dans le contexte présent.
Par contre, juste en la regardant "en diagonale", je comprend pas bien ce qu'elle est sensée calculer la formule en question vu que je vois pas trop quelle utilité pourrait avoir une racine d'un gros truc dans le contexte présent.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: formule pour densité de plantation

Avec un écart (comme sur le dessin) de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: formule pour densité de plantation
la formule absurde est sensée donner la hauteur d'un triangle qu'il soit isocèle ou rectangle.
Pour placer sur le terrain, cela donne la distance entre les lignes . C'est plus simple que de mesurer la diagonale.
Pour placer sur le terrain, cela donne la distance entre les lignes . C'est plus simple que de mesurer la diagonale.
Re: formule pour densité de plantation
Désolé, je ne comprends pas la formule à la fin de ton message. J'espère que mon ignorance ne t'agace pas 
Cette formule bizarre avec √d'un gros truc pour calculer la hauteur du triangle formées par l'implantation en quinconce est-elle juste ou pas ?
C'est un paramètre important à connaitre pour mon problème car sur le terrain, il est facile de mesurer la distance entre deux rangs pour une implantation en quinconce mais bien plus difficile de mesurer une diagonale et de tomber juste.
Pour ce qui est de l'accès au fichier pour l'affichage d'erreur, tu aurais le temps et l'envie de voir si je te le transmet par exemple par mail ?

Cette formule bizarre avec √d'un gros truc pour calculer la hauteur du triangle formées par l'implantation en quinconce est-elle juste ou pas ?
C'est un paramètre important à connaitre pour mon problème car sur le terrain, il est facile de mesurer la distance entre deux rangs pour une implantation en quinconce mais bien plus difficile de mesurer une diagonale et de tomber juste.
Pour ce qui est de l'accès au fichier pour l'affichage d'erreur, tu aurais le temps et l'envie de voir si je te le transmet par exemple par mail ?
Re: formule pour densité de plantation
Concernant la formule
}{d\!+\!e}\Big)\times E\Big(1+\dfrac{\sqrt{2}(L-d)}{d\!+\!e}\bigg)+1\bigg]\Bigg])
La racine, elle ne "porte" que sur le 2 et lien d'autre.
Ecrite "en ligne" (donc plus où moins prête pour un tableur), ça donnerais ça :
Ent( 1/2 * ( Ent( 1 + racine(2)*(l-d)/(d+e) ) * Ent( 1 + racine(2)*(L-d)/(d+e) ) + 1 ) )
Je t'ai mis les deux formules dans un petit "google sheet" là :
https://docs.google.com/spreadsheets/d/ ... sp=sharing
Si tu veut que je regarde la tienne, met là dans une des cases de la même feuille.
Sinon, je sais pas pour quelle raisons tu t’intéresse à différentes dispositions, mais si tu veut mettre le plus de plans possible en respectant un écart minimum entre les plans, je pense que l'optimum serait plutôt une disposition triangulaire :

La racine, elle ne "porte" que sur le 2 et lien d'autre.
Ecrite "en ligne" (donc plus où moins prête pour un tableur), ça donnerais ça :
Ent( 1/2 * ( Ent( 1 + racine(2)*(l-d)/(d+e) ) * Ent( 1 + racine(2)*(L-d)/(d+e) ) + 1 ) )
Je t'ai mis les deux formules dans un petit "google sheet" là :
https://docs.google.com/spreadsheets/d/ ... sp=sharing
Si tu veut que je regarde la tienne, met là dans une des cases de la même feuille.
Sinon, je sais pas pour quelle raisons tu t’intéresse à différentes dispositions, mais si tu veut mettre le plus de plans possible en respectant un écart minimum entre les plans, je pense que l'optimum serait plutôt une disposition triangulaire :
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: formule pour densité de plantation
je m'intéresse comme je t'ai dit pour le jardinage.
J'ai cherché en ligne pour quelques mètres carrés et je n'ai trouvé que des tableaux ce que j'ai trouvé restrictif car évidemment toutes les configurations sont impossibles à prévoir.
Je me suis donc dit qu'un tableur où on pourrait changer les paramètres serait plus utiles.
Oui pour la dispo en triangle, ce'st ce que j'appelle en quinconce, c'est pour cela que connaitre la hauteur du triangle (=distance entre deux rang) serait utile si cela était donné dans le tableau.
J'ai mis le mien sur ta feuille.
Je me rends compte qu'il y a moins d'élément en quinconce qu'en carré, j'aurais pensé le contraire… la formule est probablemnt fausse (avec cette formule bizarre déjà évoquée), il y a d'ailleurs une erreur de résultat en J6 J7 et L6. Ça correspond à un espacement inférieur au diamètre des plantes (si on veut que les branches s'interpénètrent pour un massif plus dense.)
J'ai cherché en ligne pour quelques mètres carrés et je n'ai trouvé que des tableaux ce que j'ai trouvé restrictif car évidemment toutes les configurations sont impossibles à prévoir.
Je me suis donc dit qu'un tableur où on pourrait changer les paramètres serait plus utiles.
Oui pour la dispo en triangle, ce'st ce que j'appelle en quinconce, c'est pour cela que connaitre la hauteur du triangle (=distance entre deux rang) serait utile si cela était donné dans le tableau.
J'ai mis le mien sur ta feuille.
Je me rends compte qu'il y a moins d'élément en quinconce qu'en carré, j'aurais pensé le contraire… la formule est probablemnt fausse (avec cette formule bizarre déjà évoquée), il y a d'ailleurs une erreur de résultat en J6 J7 et L6. Ça correspond à un espacement inférieur au diamètre des plantes (si on veut que les branches s'interpénètrent pour un massif plus dense.)
Re: formule pour densité de plantation
Concernant la dispo. en quinconce, j'était allé regardé sur le net. et les sites sur lesquels je suis tombé donnaient la dispo. du dessin du post du 13/09 ; 21:59 : c'est un carré avec un cinquième élément situé à l'intérieur du carré et les les écarts  entre les plans il sont là où ils sont marqués sur le dessin avec le centre du carré (et c'est tout). Par exemple le "triangle du bas" (du centre du carré aux deux d'en dessous), c'est un "demi carré" (avec un angle droit) et il est équilatéral mais pas isocèle (deux cotés égaux, seulement)
entre les plans il sont là où ils sont marqués sur le dessin avec le centre du carré (et c'est tout). Par exemple le "triangle du bas" (du centre du carré aux deux d'en dessous), c'est un "demi carré" (avec un angle droit) et il est équilatéral mais pas isocèle (deux cotés égaux, seulement)
Alors que sur la dispo. en triangle (voir post du 14/09 ; 21:01), les écarts ils sont partout où il y a des segments en pointillé donc le triangle du bas est équilatéral, mais par contre, si on prend les 4 plans qui correspondaient au carré dans la dispo. en quinconce, là, c'est pas un carré, mais un rectangle.
ils sont partout où il y a des segments en pointillé donc le triangle du bas est équilatéral, mais par contre, si on prend les 4 plans qui correspondaient au carré dans la dispo. en quinconce, là, c'est pas un carré, mais un rectangle.
Enfin, bref, on s'en fout un peu du nom que les dispo. portent (donc si tu veut, on peut appeler "en quinconce" celle que j'appelle "en triangle"), mais par contre, c'est pas les deux mêmes et effectivement, c'est avec celle "en triangle" que tu mettra le plus de plants (en tout cas si le rectangle de départ est un peu grand pour qu'il n'y a pas trop d'effet "de bord").
Après calculs et sauf erreur, pour une disposition en triangle, le nombre de plants c'est :
}{d\!+\!e}\bigg)-1 \bigg)\times E\bigg(1+\dfrac{2(L-d)}{\sqrt{3}(d\!+\!e)}\bigg)+1\bigg]\Bigg])
Attention au fait que la dispo. n'est plus symétrique par rapport à la diagonale donc que et
et  ne jouent plus le même rôle.
ne jouent plus le même rôle.
Je te rajoute la formule dans la (même) feuille du tableur.
EDIT : en regardant ce que tu as rajouté dans la feuille, visiblement, tu manipule deux "écarts entre plants" et
et  donc à priori, ni une "vrai" dispo. en quinconce, ni une "vrai" dispo en triangles.
donc à priori, ni une "vrai" dispo. en quinconce, ni une "vrai" dispo en triangles.
On peut évidement inventer d'autres dispositions, et je peut te trouver les formules correspondantes, mais il faudrait que ce soit parfaitement clair de savoir ce que représentent les longueur et
et  (i.e. où elles se mesurent sur un dessin)
(i.e. où elles se mesurent sur un dessin)
Alors que sur la dispo. en triangle (voir post du 14/09 ; 21:01), les écarts
Enfin, bref, on s'en fout un peu du nom que les dispo. portent (donc si tu veut, on peut appeler "en quinconce" celle que j'appelle "en triangle"), mais par contre, c'est pas les deux mêmes et effectivement, c'est avec celle "en triangle" que tu mettra le plus de plants (en tout cas si le rectangle de départ est un peu grand pour qu'il n'y a pas trop d'effet "de bord").
Après calculs et sauf erreur, pour une disposition en triangle, le nombre de plants c'est :
Attention au fait que la dispo. n'est plus symétrique par rapport à la diagonale donc que
Je te rajoute la formule dans la (même) feuille du tableur.
EDIT : en regardant ce que tu as rajouté dans la feuille, visiblement, tu manipule deux "écarts entre plants"
On peut évidement inventer d'autres dispositions, et je peut te trouver les formules correspondantes, mais il faudrait que ce soit parfaitement clair de savoir ce que représentent les longueur
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: formule pour densité de plantation
comme tu le dis, il serait bien d'avoir le même vocabulaire .
Voici une image représentant toutes les configurations avec mes propres mots.
N'hésite pas à me corriger avec des mots plus "techniques" si nécessaire.
Sur le spreadsheet j'ai mis la même image et j'ai complété le tableau.
Il est important d'avoir plusieurs entrées pour comparer les plantations composées.
Il reste à trouver la formule donnant la hauteur dans les configurations que j'appelle en triangles.
https://www.noelshack.com/2018-37-7-1537118915-00-densite-de-plantation-forum-018-0916.png

Voici une image représentant toutes les configurations avec mes propres mots.
N'hésite pas à me corriger avec des mots plus "techniques" si nécessaire.
Sur le spreadsheet j'ai mis la même image et j'ai complété le tableau.
Il est important d'avoir plusieurs entrées pour comparer les plantations composées.
Il reste à trouver la formule donnant la hauteur dans les configurations que j'appelle en triangles.
https://www.noelshack.com/2018-37-7-1537118915-00-densite-de-plantation-forum-018-0916.png

Re: formule pour densité de plantation
La hauteur  entre deux lignes (de centre de ligne à centre de ligne) sur tes cas 2 et 3, c'est
entre deux lignes (de centre de ligne à centre de ligne) sur tes cas 2 et 3, c'est ^2+\Big(\dfrac{E\!+\!d}{2}\Big)^{\!2}}) (théorème de Pythagore).
(théorème de Pythagore).
Ensuite, si tu accepte des et
et  différents, alors les cas que j'avais appelés "en quinconce" et "en triangle", rentrent tout les deux dans le moule : le cas "en triangle" est celui où
différents, alors les cas que j'avais appelés "en quinconce" et "en triangle", rentrent tout les deux dans le moule : le cas "en triangle" est celui où 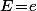 et celui "en quinconce" correspond à
et celui "en quinconce" correspond à \!-\!d) .
.
Par contre, ton dessin 2 (triangle) qui commence par une ligne contenant (éventuellement) un élément de moins que celle au dessus n'a pas vraiment d'intérêt : tu as toujours à commencer par une première ligne la plus longue possible (donc toujours mettre un plan dans le coin bas/gauche du rectangle)
Je regarderais ce soir combien on rentre de plan avec une dispo. en E - e
Ensuite, si tu accepte des
Par contre, ton dessin 2 (triangle) qui commence par une ligne contenant (éventuellement) un élément de moins que celle au dessus n'a pas vraiment d'intérêt : tu as toujours à commencer par une première ligne la plus longue possible (donc toujours mettre un plan dans le coin bas/gauche du rectangle)
Je regarderais ce soir combien on rentre de plan avec une dispo. en E - e
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: formule pour densité de plantation
le calcul de la hauteur traduit en formule ods c'est bien
"h=racine( ( (e+d) * (e+d) ) + ( ((E+d) /2) * ((E+d) /2) ) )" ?
sur wikipédia je trouve h = E × ((√3) / 2) c'est bien la même chose ?
En tout cas la formule semble donner un résultat cohérent pour les triangles équilatérales donc avec bien sûr E = e (en triangle).
Pour les isocèles donc avec E ≠ e (en quinconce), on a deux cas d'isocèle avec E < e (j'appelle ça triangle haut) et E > e (triangle plat)
La formule trouvé sur wikipédia est h=(1/2)*(√4*e²-E²
en formule ods c'est bien (1/2) * (racine ( ((4 * (e*e)) – (E*E))) ?
si oui ça semble marcher pour les triangles E < e mais pas avec E > e
pourquoi ?
J'ai modifié mon dessin pour nommer les figures.
- Rectangle : fig 1
- Triangle équilatéral : fig 2
- Triangle isocèle haut : fig 2h (E < e)
- Triangle isocèle plat : fig E > e)
Pour moi la première ligne est celle du haut j'avais mis un dessin où la première ligne était plus petite pour montrer un cas de figure inhabituel mais effectivement ça change rien j'ai donc modifié pour avoir une première ligne pleine.
"h=racine( ( (e+d) * (e+d) ) + ( ((E+d) /2) * ((E+d) /2) ) )" ?
sur wikipédia je trouve h = E × ((√3) / 2) c'est bien la même chose ?
En tout cas la formule semble donner un résultat cohérent pour les triangles équilatérales donc avec bien sûr E = e (en triangle).
Pour les isocèles donc avec E ≠ e (en quinconce), on a deux cas d'isocèle avec E < e (j'appelle ça triangle haut) et E > e (triangle plat)
La formule trouvé sur wikipédia est h=(1/2)*(√4*e²-E²
en formule ods c'est bien (1/2) * (racine ( ((4 * (e*e)) – (E*E))) ?
si oui ça semble marcher pour les triangles E < e mais pas avec E > e
pourquoi ?
J'ai modifié mon dessin pour nommer les figures.
- Rectangle : fig 1
- Triangle équilatéral : fig 2
- Triangle isocèle haut : fig 2h (E < e)
- Triangle isocèle plat : fig E > e)
Pour moi la première ligne est celle du haut j'avais mis un dessin où la première ligne était plus petite pour montrer un cas de figure inhabituel mais effectivement ça change rien j'ai donc modifié pour avoir une première ligne pleine.
Re: formule pour densité de plantation
Avec ça comme configuration (en cliquant dessus, ça agrandit un peu et on voit mieux où sont  et
et  que j'ai bêtement mis en jaune trop clair) :
que j'ai bêtement mis en jaune trop clair) :

Sur le dessin çi dessus, (où tu as forcément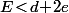 ), la hauteur
), la hauteur  c'est
c'est
^2-\Big(\dfrac{E\!+\!d}{2}\Big)^{\!2}}) (*) c'est à dire h=racine( (e+d)^2 - ( (E+d)/2)^2 )
(*) c'est à dire h=racine( (e+d)^2 - ( (E+d)/2)^2 )
(sauf erreur, tout les tableurs savent calculer des puissances et le symbole dédié, c'est ^)
Et la formule h = E × ((√3) / 2, c'est celle pour les triangle équilatéraux (i.e.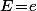 ) et elle ne tient pas compte du diamètre
) et elle ne tient pas compte du diamètre  .
.
Et, sauf erreur, pour une telle disposition, le nombre de plants c'est ça :
\times E\bigg(1+\dfrac{\ell-d}{h}\bigg)+1\bigg]\Bigg]) c'est à dire
c'est à dire
N = ENT( 1/2 * ( Ent(1+2*(L-d)/(E+d)) * Ent(1+2*(l-d)/h) + 1 ) ) où h est à calculer avec la formule ci dessus.
(*) Et j'avais écrit une c.. dans le précédent post où j'avais mis un + et pas un -

Sur le dessin çi dessus, (où tu as forcément
(sauf erreur, tout les tableurs savent calculer des puissances et le symbole dédié, c'est ^)
Et la formule h = E × ((√3) / 2, c'est celle pour les triangle équilatéraux (i.e.
Et, sauf erreur, pour une telle disposition, le nombre de plants c'est ça :
N = ENT( 1/2 * ( Ent(1+2*(L-d)/(E+d)) * Ent(1+2*(l-d)/h) + 1 ) ) où h est à calculer avec la formule ci dessus.
(*) Et j'avais écrit une c.. dans le précédent post où j'avais mis un + et pas un -
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 12 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
