Exponentiel de pure immaginaire

[maxence6]

Bonjour,
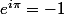
J'ai du mal à saisir pourquoi parce que si jusque là ça va mais si on développe:




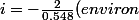Mais comme i n'est pas égal 2/0.548 je me demande ce qui cloche aidez moi encore une fois de plus s'il vous plait

[fatal_error]

salut,

en fait, sin(pi) ca vaut 0.

[maxence6]

A bon pourquoi, quand on le tape sur une machine on a environ 0.05 et si dans un cercle trigonométrique on prend un angle de environ 3.14 on voit bien que se n'est pas égal a zero

[Arnaud-29-31]

Ta calculatrice doit être en degré ...
Lorsque l'on met une fraction de sous un cos ou un sin, cela sous entend que l'on parle en radians.

D'ailleurs en math, à partir de la seconde, on n'utilise quasiment plus jamais les degrés ...

[maxence6]

A d'accord donc en faite le égal -1 est en radian et non en degrès ?

[maxence6]

J'ai mis ma calculette en radian je tape sin de pi et la je trouve 3.140018715.. enfin apart le début le reste ne ressemble pas aux décimales de pi

[Arnaud-29-31]

-1 n'est pas un angle, attention un cos ou un sin te donne un rapport de distance donc un nombre sans dimension donc pas d'unité.
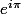
C'est le dans qui est en radians.

En réalité, radians = 180°

Tu peux donc faire le test avec avec 180 un angle en degrés.

[Arnaud-29-31]

J'ai mis ma calculette en radian je tape sin de pi et la je trouve 3.140018715.. enfin apart le début le reste ne ressemble pas aux décimales de pi

Pour , tu dois en principe trouver 0 si ta calculatrice en bien en radians.

[Micki28]

Bonjour,

Regardes tout simplement le cercle trigonométrique, tu vois bien où se situe l'angle Pi !

Donc tu vois bien que le cosinus est égal à -1 et le sinus est égal à 0

Donc:

cos (Pi) + i sin (Pi) = -1 + i*0 = -1

Et comme la forme trigonométrique peut se mettre en forme exponentielle ça donne:

e^iPi = -1

Et on a donc l'identité d'Euler: e^iPi + 1 = 0

Qui regroupe des nombres importants des mathématiques: e, i, Pi, 1

[maxence6]

Oui maintenant je vois ou se situe l'angle pi mais au début je pensé en degrès alors que c'était pi en radians