Division par 0

par **ewok31** » 28 Mar 2012, 15:57

Bonjour j'ai toujours crus que la division par zéro était impossible or un copain m'a dit ce matin que la division par zéro était réalisable mais qu'on la considérait comme impossible à notre niveau.
Est ce vrai?

par **Monsieur23** » 28 Mar 2012, 17:17

Aloha,

Dans le sens « J'prends un nombre, et hop, j'le divise par zéro », non ça n'existe pas.

Par contre, tu peux calculer des limites de fractions où le dénominateur tend vers 0, ce genre de trucs

par **Jota Be** » 28 Mar 2012, 17:24

ewok31 a écrit:Bonjour j'ai toujours crus que la division par zéro était impossible or un copain m'a dit ce matin que la division par zéro était réalisable mais qu'on la considérait comme impossible à notre niveau.
Est ce vrai?

Salut,
D'après ce que j'en sais, seul Chuck Norris peut parfaitement DIVISER par 0. Sinon, je ne pense pas que l'on puisse effectuer cette opération. Mais comme Monsieur23 l'a dit, on peut faire tendre le dénominateur vers 0 pour obtenir un résultat qui tend vers Chuck Norris.

par **vincentroumezy** » 28 Mar 2012, 17:27

D'ailleurs on voit bien que c'est un non sens:
0x1=0x2, donc 1/2=0/0, mais aussi 2=0/0, donc 1/2=2 ???????

par **ewok31** » 28 Mar 2012, 17:39

ok merci je crois que j'ai à peu près bien compris

par **Dlzlogic** » 28 Mar 2012, 18:23

ewok31 a écrit:ok merci je crois que j'ai à peu près bien compris

J'en rajouterai une couche dans la logique de Vincentroumezy.
La définition de la divisions est la suivante :
Diviser un nombre A par un nombre B c'est trouver un nombre Q et un nombre R tels que A=BQ+R.
[EDIT]
Mon intervention n'apporte rien, j'ai oublié dans la définition "B différent de 0" :hum:

par **Skullkid** » 28 Mar 2012, 18:37

Dlzlogic a écrit:La définition de la divisions est la suivante :
Diviser un nombre A par un nombre B c'est trouver un nombre Q et un nombre R tels que A=BQ+R.

Décidément t'es en forme aujourd'hui...

Donc en écrivant 1 = 0*2 + 1 j'ai trouvé tes nombres, donc j'ai divisé 1 par 0, c'est donc tout à fait possible d'après ta définition.

par **Dlzlogic** » 28 Mar 2012, 18:56

Skullkid a écrit:Décidément t'es en forme aujourd'hui...

Donc en écrivant 1 = 0*2 + 1 j'ai trouvé tes nombres, donc j'ai divisé 1 par 0, c'est donc tout à fait possible d'après ta définition.

Oui, t'as raison.
Pardon, là y'a un truc qui m'échappe. :hum:
Peut-être dans la définition j'ai oublié "différent de 0", en ce cas mon rajout n'apporte rien.
Si c'est le cas, je vais supprimer, ou plutôt faire un rajout.
En tout cas, merci de l'avoir vu.

par **Skullkid** » 28 Mar 2012, 19:35

C'est toujours faux si tu rajoutes B différent de 0 (en écrivant 2 = 1*0 + 2 je divise 2 par 1 d'après ta définition). Une version possible, corrigée, de ce à quoi tu pensais probablement c'est :

Effectuer la division euclidienne d'un entier A par un entier B c'est trouver deux entiers Q et R tels que A = BQ + R et R est un entier positif strictement inférieur à B. (lorsque le couple (Q,R) existe, celui-ci est unique)

Avec cette définition il est impossible de faire une division euclidienne par 0. Après, quand on dit que la division par 0 est impossible, on ne parle pas (que) de la division euclidienne, mais de la division des réels, qui a une autre définition.

par **Dlzlogic** » 28 Mar 2012, 19:41

OK, évidemment, je suis bête, s'il y a un reste, ça ne peux concerner que des entiers. Comme tu dis, j'ai pas la forme aujourd'hui.
Ma box marque 19H0, mais il est 20H40. J'ai toujours eu du mal avec les heures.

par **blette** » 03 Avr 2012, 18:03

la division par 0 semblerait valoir l'infini si on travaille avec les limites. Vive moi! et pour en rajouter une couche par -0- l'infini Signé elie zaraya mettez a jour vos calculatrices!

par **Judoboy** » 03 Avr 2012, 18:09

blette a écrit:la division par 0 semblerait valoir l'infini si on travaille avec les limites. Vive moi!

Bah ça y est tu l'as ta médaille Fields.

par **leon1789** » 03 Avr 2012, 18:12

Dlzlogic a écrit:OK, évidemment, je suis bête, s'il y a un reste, ça ne peux concerner que des entiers.

Pas uniquement les entiers, il y a aussi une division euclidienne pour les polynômes à coefficients dans un corps : division de x^3+2x+2 par 3x^2+3 --> quotient = x/3 , reste = x+2
On peut aussi définir une division "archimidienne" sur les réels en précisant que le quotient doit être un nombre entier : division de 4.52 par 2.1 --> quotient = 2 , reste = 0.32

par **couleuvre** » 06 Avr 2012, 15:06

si on fait une fonction sur un graphe avec un dénominateur tendant vers 0 par logique déductive on peut admettre que si le dénominateur valait 0 cela vaudrait + l'infini

par **Dlzlogic** » 06 Avr 2012, 15:17

couleuvre a écrit:si on fait une fonction sur un graphe avec un dénominateur tendant vers 0 par logique déductive on peut admettre que si le dénominateur valait 0 cela vaudrait + l'infini

Non. On dit que si x tend vers 0, alors 1/x tend vers oo. Mais pas plus.
Rien ne peut "valoir + infini" sinon +oo +1 = +oo d'où 1=0.
Toute tentative de dire que quelque-chose vaut l'infini ou est égal à l'infini conduit à des aberrations.

par **Sylviel** » 06 Avr 2012, 15:38

Toute tentative de dire que quelque-chose vaut l'infini ou est égal à l'infini conduit à des aberrations.

C'est vrai pour une première approche. Cependant dans certaines branche des maths (dont l'analyse convexe, et l'optimisation de manière générale) on a introduit des fonctions valant +oo (et parfois -oo). C'est tout a fait possible, et ça à de l'intérêt, mais il faut effectivement être très prudent dans les règles que l'on se donne pour étendre addition, multiplication et division.

par **Dlzlogic** » 06 Avr 2012, 15:46

Oui, sûrement, mais est-ce que ça répond aux premières questions ?

par **Mortelune** » 06 Avr 2012, 23:20

En algèbre on peut définir quelque chose qui ressemble à une division par 0, par contre il vaut mieux avoir vu les anneaux.
Sur wiki ici

Une partie du dernier point des exemples importants se rattache à la question, si f est nilpotent (donc qu'une puissance de f s'annule donc que 0 appartienne à la partie multiplicative S - définie comme l'ensemble des puissance de f -) la localisation rendra en particulier 0 inversible, on aura donc défini une division par 0. Mais le fait que 0 appartienne à S implique que l'ensemble obtenu par le procédé de localisation est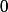

. Donc on a divisé par 0.
Et je suis d'accord pour dire que ce n'est pas vraiment utile de savoir ça au lycée.

Une démonstration à partir de la relation d'équivalence :

On a alors toujours (si

)

puisque 0(1a-0s)=0. Donc en particulier, si on note :

on aura

(c'est la notation adoptée pour les rationnels par exemple).

par **Dlzlogic** » 07 Avr 2012, 10:55

Bonjour,
A mon avis, ceci apportera une réponse très claire à nodjim
http://www.maths-forum.com/ensemble-entiers-naturels-125540.php

par **leon1789** » 07 Avr 2012, 11:45

Mortelune a écrit:Une partie du dernier point des exemples importants se rattache à la question, si f est nilpotent (donc qu'une puissance de f s'annule donc que 0 appartienne à la partie multiplicative S - définie comme l'ensemble des puissance de f -) la localisation rendra en particulier 0 inversible, on aura donc défini une division par 0. Mais le fait que 0 appartienne à S implique que l'ensemble obtenu par le procédé de localisation est . Donc on a divisé par 0.
Et je suis d'accord pour dire que ce n'est pas vraiment utile de savoir ça au lycée.

En clair, tu es en train de dire que le seul anneau dans lequel on peut diviser par 0 est l'anneau {0}. Ok.

Division par 0

Division par 0

par calcul des limites

logique

Qui est en ligne