Distance de Manhattan et distance Euclidienne.
17 messages
- Page 1 sur 1
Distance de Manhattan et distance Euclidienne.
Bonjour,
La notion de distance de Manhattan en été évoquée 2 fois dernièrement sur ce forum.
Rappel, la distance Euclidienne est la plus courte distance entre deux points, appelée aussi distance à vol d'oiseau, c'est la racine carrée de la somme des carrés des différences de coordonnées en X et en Y.
La distance de Manhattan est égale à la somme des valeurs absolues des différences de coordonnées en X et en Y. Il est évident que la mesure de la distance de Manhattan est plus grande (ou égale) que celle de la distance Euclidienne.
Je pense que cette notion a été inventée dans le contexte SIG.
Il est en effet intéressant de pouvoir calculer la distance d'un point à un autre, telle qu'aurait à la parcourir un taxi dans une ville, et non une distance à vol d'oiseau.
Il est aussi possible de calculer le chemin d'un point à un autre en suivant les rues. Ce calcul est relativement long et difficile, mais est-il bien utile lorsqu'on ne cherche que la distance, et pas l'itinéraire ?
En supposant qu'il n'y ait ni passage obligé, type pont, ni sens interdit, si on appelle E la distance Euclidienne et M la distance de Manhattan, E <= M <= E x 1.414.
Sur un grand nombre de calculs, M tend vers E x (cos(22.5°) + sin(22.5°) ) = E x 1.307.
Il en résulte, à mon avis, que la valeur d'une distance en passant par des trajets obligés mais inconnu peur être obtenue avec une bonne approximation en multipliant la distance Euclidienne pas 1.3.
Qu'en pensez-vous ? Quelqu'un a-t-il déjà été confronté à ce type de problème ?
La notion de distance de Manhattan en été évoquée 2 fois dernièrement sur ce forum.
Rappel, la distance Euclidienne est la plus courte distance entre deux points, appelée aussi distance à vol d'oiseau, c'est la racine carrée de la somme des carrés des différences de coordonnées en X et en Y.
La distance de Manhattan est égale à la somme des valeurs absolues des différences de coordonnées en X et en Y. Il est évident que la mesure de la distance de Manhattan est plus grande (ou égale) que celle de la distance Euclidienne.
Je pense que cette notion a été inventée dans le contexte SIG.
Il est en effet intéressant de pouvoir calculer la distance d'un point à un autre, telle qu'aurait à la parcourir un taxi dans une ville, et non une distance à vol d'oiseau.
Il est aussi possible de calculer le chemin d'un point à un autre en suivant les rues. Ce calcul est relativement long et difficile, mais est-il bien utile lorsqu'on ne cherche que la distance, et pas l'itinéraire ?
En supposant qu'il n'y ait ni passage obligé, type pont, ni sens interdit, si on appelle E la distance Euclidienne et M la distance de Manhattan, E <= M <= E x 1.414.
Sur un grand nombre de calculs, M tend vers E x (cos(22.5°) + sin(22.5°) ) = E x 1.307.
Il en résulte, à mon avis, que la valeur d'une distance en passant par des trajets obligés mais inconnu peur être obtenue avec une bonne approximation en multipliant la distance Euclidienne pas 1.3.
Qu'en pensez-vous ? Quelqu'un a-t-il déjà été confronté à ce type de problème ?
Quand on parle de distance entre deux points de la surface du globe, il y a en fait deux types de distance : une distance rectiligne qui passe dans l'écorce terrestre et qui relie les deux points, et une autre distance qui suit la courbure quasi-sphérique de la Terre. Pour jongler avec la géométrie entre trois dimensions, on construit un repère x,y,z, c'est-à-dire des coordonnées spatiales.
Voici le système déquations permettant de convertir la longitude et la latitude en coordonnées cartésiennes :
x = R × cos l × sin L
y = R × cos l × cos L
z = R × sin l
L = longitude
l = latitude
R = rayon terrestre = 6371 km (rayon volumétrique de référence)
La distance rectiligne (notée D) est la distance la plus courte entre deux points du globe, telle que D² = (x a)² + (y b)² + (z c)² où x,y,z et a,b,c désignent les coordonnées 3D respectives des deux points.
Langle A (en radians) entre deux points (via le centre de la Terre) est exprimé ainsi :
A = 2 × arcsin (D / (2R))
La distance géodésique (notée G) est la distance courbe qui suit la rotondité terrestre, telle que G = A × R = 2 × R × arcsin (D / (2R))
:++:
Voici le système déquations permettant de convertir la longitude et la latitude en coordonnées cartésiennes :
x = R × cos l × sin L
y = R × cos l × cos L
z = R × sin l
L = longitude
l = latitude
R = rayon terrestre = 6371 km (rayon volumétrique de référence)
La distance rectiligne (notée D) est la distance la plus courte entre deux points du globe, telle que D² = (x a)² + (y b)² + (z c)² où x,y,z et a,b,c désignent les coordonnées 3D respectives des deux points.
Langle A (en radians) entre deux points (via le centre de la Terre) est exprimé ainsi :
A = 2 × arcsin (D / (2R))
La distance géodésique (notée G) est la distance courbe qui suit la rotondité terrestre, telle que G = A × R = 2 × R × arcsin (D / (2R))
:++:
Je voudrais tout de même préciser le domaine dans lequel on peut comparer distances Euclidiennes et distances de Manhattan.
Disons que le rayon d'action est de quelques Km.
Concernant les mesures de distance sur la terre, plus grandes que quelques km, le problème est un peu compliqué et dépassé largement le cadre de cette discussion en particulier et de ce forum en général.
Toute explication limitée à quelques lignes et quelques formules ne peut être qu'incomplète.
Disons que le rayon d'action est de quelques Km.
Concernant les mesures de distance sur la terre, plus grandes que quelques km, le problème est un peu compliqué et dépassé largement le cadre de cette discussion en particulier et de ce forum en général.
Toute explication limitée à quelques lignes et quelques formules ne peut être qu'incomplète.
Dlzlogic a écrit:Sur un grand nombre de calculs, M tend vers E x (cos(22.5°) + sin(22.5°) ) = E x 1.307.
J'imagine que ce que tu veux dire par là c'est que tu as pris au hasard un grand nombre de couples de points dans un certain domaine (lequel ? un carré ? un disque ? une calotte sphérique ?), que tu as calculé la moyenne (et non pas la limite, ce qui n'a pas de sens ici) du rapport M/E sur ces tirages, et que tu as obtenu 1,307.
Si un point est tiré uniformément dans un domaine plan, l'espérance du rapport M/E, où M et E désignent les distances entre ce point et une origine fixée à l'avance (deux axes doivent aussi être fixés pour pouvoir calculer la distance de Manhattan, qui n'est pas indépendante du choix d'axes), vaut
Si on fait le tirage dans un disque centré sur l'origine,
Si on change de domaine ou de méthode de tirage (par exemple en tirant un couple de points au lieu d'un seul point) ça va faire changer l'espérance. Si le domaine est une partie de la sphère, la formule avec l'intégrale n'est pas valable (et de toute façon les coordonnées polaires n'existent pas sur la sphère).
Bonjour Skullkid,
Oh, non, c'est beaucoup plus simple que tout cela.
Je pensais l'avoir bien expliqué dans mon premier post.
L'un des buts d'un SIG (Système d'Information Géographique) est de calculer une ou des distances.
S'il s'agit de calculer LA distance que devra parcourir le véhicule de secours pour se rendre au lieu du sinistre, là on utilisera la logique de l'itinéraire, et la distance sera la somme des distances élémentaires.
Par contre s'il s'agit d'évaluer des temps de parcourt (fonction de la distance et de la vitesse) pour une société de taxi, il faut trouver une technique différente, c'est ce que j'ai essayé d'expliquer.
Il est bien évident que la distinction entre "surface plane ou surface sphérique " est sans objet.
Quand j'ai vu cette notion de "distance de Manhattan" je me suis demandé à quoi ça pouvait servir. Ta remarque concernant la direction des axes est aussi sans objet, parce qu'alors cette nouvelle notion serait parfaitement inutile.
Tu parles de "moyenne", oui, la direction moyenne entre le point de départ de le point d'arrivée est 22.5°. Mais j'aurais naturellement dû me limiter à 2 chiffres significatifs, c'est à dire un rapport M/E=1.3.
S'il y a une autre utilité à la notion de distance de Manhattan, ça m'intéresse, puisque c'est le but de ce nouveau sujet.
Oh, non, c'est beaucoup plus simple que tout cela.
Je pensais l'avoir bien expliqué dans mon premier post.
L'un des buts d'un SIG (Système d'Information Géographique) est de calculer une ou des distances.
S'il s'agit de calculer LA distance que devra parcourir le véhicule de secours pour se rendre au lieu du sinistre, là on utilisera la logique de l'itinéraire, et la distance sera la somme des distances élémentaires.
Par contre s'il s'agit d'évaluer des temps de parcourt (fonction de la distance et de la vitesse) pour une société de taxi, il faut trouver une technique différente, c'est ce que j'ai essayé d'expliquer.
Il est bien évident que la distinction entre "surface plane ou surface sphérique " est sans objet.
Quand j'ai vu cette notion de "distance de Manhattan" je me suis demandé à quoi ça pouvait servir. Ta remarque concernant la direction des axes est aussi sans objet, parce qu'alors cette nouvelle notion serait parfaitement inutile.
Tu parles de "moyenne", oui, la direction moyenne entre le point de départ de le point d'arrivée est 22.5°. Mais j'aurais naturellement dû me limiter à 2 chiffres significatifs, c'est à dire un rapport M/E=1.3.
S'il y a une autre utilité à la notion de distance de Manhattan, ça m'intéresse, puisque c'est le but de ce nouveau sujet.
Moi je ne trouve cela pas très clair...
Que signifie :
Ce que tu appelles la distance de Manhattan est en fait la distance issue de la norme L1. En proba c'est celle qui donneras la médiane par exemple (on minimise E | X - m |). Elle apparaît naturellement dans un certain nombre de problèmes industriel, mais à des propriétés mathématiques plutôt désagréable.
Que signifie :
Sur un grand nombre de calculs, M tend vers E x (cos(22.5°) + sin(22.5°) ) = E x 1.307.
Ce que tu appelles la distance de Manhattan est en fait la distance issue de la norme L1. En proba c'est celle qui donneras la médiane par exemple (on minimise E | X - m |). Elle apparaît naturellement dans un certain nombre de problèmes industriel, mais à des propriétés mathématiques plutôt désagréable.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Dlzlogic a écrit:Bonjour Skullkid,
Oh, non, c'est beaucoup plus simple que tout cela.
Bah tu parlais de "convergence", ce qui n'a aucun sens ici, donc j'ai essayé de deviner ce que tu voulais dire par là et j'ai exposé le problème (enfin ce que j'ai pu en deviner) sous un angle théorique, avec des réponses théoriques.
Dlzlogic a écrit:Il est bien évident que la distinction entre "surface plane ou surface sphérique " est sans objet.
Ah bon ? Pourtant ça change toute la géométrie, donc les distances. Comme je l'ai expliqué dans mon précédent post, tu changes la surface, tu changes la moyenne du rapport M/E.
Dlzlogic a écrit:Ta remarque concernant la direction des axes est aussi sans objet, parce qu'alors cette nouvelle notion serait parfaitement inutile.
Gné ? Ce n'est pas parce que la distance de Manhattan dépend d'un choix d'axes qu'elle est inutile. À un problème donné va correspondre un ou plusieurs systèmes d'axes "adaptés". Si on se balade dans un quadrillage, la distance de Manhattan qui vient d'abord à l'esprit est évidemment celle dont les axes sont ceux du quadrillage, mais ce n'est pas la seule qu'on peut considérer. Par exemple aux échecs, la distance de Manhattan dont les axes sont parallèles aux bords de l'échiquier est adaptée au déplacement des tours, alors que le déplacement des fous se traite mieux dans un système d'axes incliné à 45° par rapport au précédent.
Dlzlogic a écrit:Tu parles de "moyenne", oui, la direction moyenne entre le point de départ de le point d'arrivée est 22.5°. Mais j'aurais naturellement dû me limiter à 2 chiffres significatifs, c'est à dire un rapport M/E=1.3.
J'ai parlé de moyenne parce que j'ai essayé de deviner ce que tu voulais dire par "tend vers". Mais je ne sais toujours pas si tu as fait ta moyenne en partant d'une simulation aléatoire ou en partant de mesures. Si c'est une simulation aléatoire, les chiffres significatifs n'ont aucun sens : la moyenne que tu as obtenue est la moyenne que tu as obtenue. Dans tous les cas, cette moyenne va dépendre du contexte.
Dlzlogic a écrit:S'il y a une autre utilité à la notion de distance de Manhattan, ça m'intéresse, puisque c'est le but de ce nouveau sujet.
On s'en sert principalement dès que les problèmes concernent un réseau ("quadrillage" à n'importe quel nombre de dimensions), puisque c'est la distance adaptée aux réseaux. Naturellement ça n'est pas limité aux applications géographiques (d'ailleurs je ne pense pas que le concept ait été formalisé pour ça à l'origine, mais qui sait).
Comme c'est une distance, on peut l'utiliser pour modéliser un écart, une différence. Par exemple on peut comparer deux fonctions (une représentant une simulation et l'autre une mesure) de cette façon (dans ce cas on parle plutôt de distance L1, qui est le nom matheux donné à cette distance). C'est aussi une distance utilisée en transmission du signal, pour faire des codes résistants aux erreurs par exemple (la distance de Manhattan entre signaux binaires est le nombre de bits erronés dans le signal d'arrivée, comparativement au signal de départ).
Enfin, elle a des applications théoriques, la distance L1 définit une "géométrie" particulière sur certains espaces. Elle est par exemple utilisée en probas (la médiane d'une variable aléatoire X est la valeur m qui minimise la distance L1 entre X et m).
Bon, alors j'ai appris quelque-chose, c'est d'ailleurs le but d'un forum et naturellement le but de ce topic
.
Je résume : "la distance de Manhattan, dont le vrai nom est "distance L1" est utilisée pour des quantités de choses que le ne connais pas, on ne sait pas l'origine de cette appellation et elle apparait dans un certain nombre de problèmes industriels mais a des propriétés mathématiques plutôt désagréables".
Merci.
.
Je résume : "la distance de Manhattan, dont le vrai nom est "distance L1" est utilisée pour des quantités de choses que le ne connais pas, on ne sait pas l'origine de cette appellation et elle apparait dans un certain nombre de problèmes industriels mais a des propriétés mathématiques plutôt désagréables".
Merci.
L'origine des appellations on les connaît. J'imagine que je n'ai pas besoin d'expliquer l'origine du nom "distance de Manhattan" (ou d'autres noms genre "taxi-distance")... Pour la culture, le L dans "distance L1" est en l'honneur du mathématicien Henri Lebesgue qui a formalisé une théorie de l'intégration. En fait, cette théorie fournit un certain nombre d'espaces de fonctions (au sens large qui inclut les suites et les n-uplets) qu'on a nommés "espaces 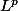 ". Un espace
". Un espace 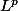 est un ensemble de fonctions dont la puissance d'exposant p est Lebesgue-intégrable. Ces espaces se munissent naturellement d'une distance, dite distance
est un ensemble de fonctions dont la puissance d'exposant p est Lebesgue-intégrable. Ces espaces se munissent naturellement d'une distance, dite distance 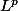 :
: ^{\frac{1}{p}}) . Le cas p = 1 est celui qui nous concerne ici, le cas p = 2 est la distance euclidienne usuelle, les autres cas sont moins souvent utilisés (sauf le cas p = infini qui est un peu particulier).
. Le cas p = 1 est celui qui nous concerne ici, le cas p = 2 est la distance euclidienne usuelle, les autres cas sont moins souvent utilisés (sauf le cas p = infini qui est un peu particulier).
Mais on n'a probablement pas attendu l'arrivée de Lebesgue pour calculer des distances dans des réseaux, donc cette distance a sans doute été utilisée avant d'être complètement formalisée et généralisée.
Mais on n'a probablement pas attendu l'arrivée de Lebesgue pour calculer des distances dans des réseaux, donc cette distance a sans doute été utilisée avant d'être complètement formalisée et généralisée.
L'avantage de connaitre le nom que les mathématiciens utilise pour ce qui t'intéresse en ce moment (a savoir la norme L1) c'est que tu as tout internet pour trouver par toi même les renseignements que tu veux. Skullkid t'as donné un certain nombre d'exemples pratique d'utilisation de cette distance (réseaux, codes correcteurs...). Je t'ai donné un cas où elle se relie à une notion que tu connais déjà (la médiane), etc... maintenant si tu veux rester condescendant et ironique, fais toi plaisir.
Après si tu veux que j'argumente mes propos pas de problèmes :
- elle est non différentiable
- l'espace de banach des fonctions L1 munie de cette norme est non reflexif, et son dual n'est pas séparable
Je suis sûr que savoir ça te fait une belle jambe. En revanche savoir qu'elle a des propriétés mathématiques désagréables qui compliquent la vie de ceux qui veulent l'utiliser (même si elle est bien étudiée et maîtrisée) ne me semblait pas si inutile que ça à dire...
Après si tu veux que j'argumente mes propos pas de problèmes :
- elle est non différentiable
- l'espace de banach des fonctions L1 munie de cette norme est non reflexif, et son dual n'est pas séparable
Je suis sûr que savoir ça te fait une belle jambe. En revanche savoir qu'elle a des propriétés mathématiques désagréables qui compliquent la vie de ceux qui veulent l'utiliser (même si elle est bien étudiée et maîtrisée) ne me semblait pas si inutile que ça à dire...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Je t'ai donné un cas où elle se relie à une notion que tu connais déjà (la médiane), etc... maintenant si tu veux rester condescendant et ironique, fais toi plaisir.
Je ne sais pas ce que je t'ai fait ...
"La médiane", c'est une notion que j'ai découverte dernièrement, à l'occasion d'exercices non compris par des élèves (sur ce présent forum). Pour essayer de suivre la discussion, j'ai même demandé, par MP de peur du ridicule, de quoi il s'agissait, la définition sur Wiki ne m'éclairait pas.
On ne peut pas dire que je la connaisse, puisque je n'ai pas (encore) compris sa signification. En d'autres terme j'ai retenu le nom, que c'est à peu près au milieu, mais je sais toujours pas au milieu de quoi.
Je ne vois vraiment pas ce qui peut te faire croire que je veuille "rester condescendant et ironique".
Il est vrai que j'ai découvert ce terme (Manhattan) il y a quelques années lorsque je me suis remis aux SIG et à l'occasion de lecture sur Wiki. Donc bêtement j'ai fait la liaison (hypothétique) entre ces deux notions, d'autant que nulle part ailleurs je n'ai trouvé de références à d'autres utilisations. Ce que j'ai dit strictement mon premier post.
Autrefois on différenciait "logique" et "analogique" maintenant, on dit "discret" et "???" (là je sais pas). Admet que de temps en temps je puisse avoir du mal à comprendre et/ou à me faire comprendre.
Autrefois, on disait "tend vers" maintenant, on dit "converge", avant "parallèle" maintenant "colinéaire" avant "linéaire" maintenant "affine", mais ça n'empêche pas l'appeler "linéaire" la formule de régression qui est une fonction affine et d'écrire qu'il existe aussi des formules de régression affine etc.
Ton dernier post avait un ton très ironique. Il dis "j'ai appris quelque chose" puis sous entends que l'on ne t'a apporté aucune information et que tu restes sur ta faim.
Je pensais vraiment que tu savais ce qu'étais la médiane :triste: Pour info la médiane c'est la valeur qui sépare en deux part égale une population. Exemple : on regardes la taille d'une classe d'élève. La médiane sera la taille h tel qu'il y ai 15 élèves plus petit que h et 15 plus grand que h.
Je ne sais pas à quoi correspond logique et analogique. En général on sépare discret et continu. Tends vers et converge sont synonyme, et l'ont toujours été (on trouve les deux dans des articles des années 60). Parallèle et colinéaire sont très liés mais correspondent à deux objets différents (droites ou plans dans le premier cas, vecteurs dans le second) : je parierais donc plus sur une imprécision dans ton esprit qu'une évolution du langage. Linéaire et affine sont deux choses différentes (on en a déjà longuement parlé), mais très liées (une fonction affine est simplement une fonction linéaire + une constante) et là encore cela n'a pas évolué sur le dernier demi-siècle.
Je pensais vraiment que tu savais ce qu'étais la médiane :triste: Pour info la médiane c'est la valeur qui sépare en deux part égale une population. Exemple : on regardes la taille d'une classe d'élève. La médiane sera la taille h tel qu'il y ai 15 élèves plus petit que h et 15 plus grand que h.
Je ne sais pas à quoi correspond logique et analogique. En général on sépare discret et continu. Tends vers et converge sont synonyme, et l'ont toujours été (on trouve les deux dans des articles des années 60). Parallèle et colinéaire sont très liés mais correspondent à deux objets différents (droites ou plans dans le premier cas, vecteurs dans le second) : je parierais donc plus sur une imprécision dans ton esprit qu'une évolution du langage. Linéaire et affine sont deux choses différentes (on en a déjà longuement parlé), mais très liées (une fonction affine est simplement une fonction linéaire + une constante) et là encore cela n'a pas évolué sur le dernier demi-siècle.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
C'est tout à fait exact, je n'avais vu nulle part d'autre définition ou d'utilisation de cette "distance". J'ai appris depuis un bout de temps que le ton ironique était à éviter à tout pris dans le contexte internet. S'il m'arrive de l'employer, je l'agrémente toujours d'un smiley.Sylviel a écrit:Ton dernier post avait un ton très ironique. Il dis "j'ai appris quelque chose" puis sous entends que l'on ne t'a apporté aucune information et que tu restes sur ta faim.
Ok, mais j'ai lu aussi que c'était la valeur du plus grand nombre, c'est à dire que dans une classe de terminale, la médiane est 18 ans, parce que par exemple le plus grand nombre a 18 ans.Je pensais vraiment que tu savais ce qu'étais la médiane :triste: Pour info la médiane c'est la valeur qui sépare en deux part égale une population. Exemple : on regardes la taille d'une classe d'élève. La médiane sera la taille h tel qu'il y ai 15 élèves plus petit que h et 15 plus grand que h.
Exemple typique, une montre à aiguille est du type analogique, à affichage numérique du type logique.Je ne sais pas à quoi correspond logique et analogique.
Distance Euclidienne --> analogique ; distance de Manhattan --> logique
Entiers --> logique ; flottant --> analogique.
Binaire, digital --> logique etc..
En l'occurrence, j'ai croisé l'ancien prof de math de mon fils, je lui ai raconté ce point, et il m'a dit que ce n'était qu'un problème de terminologie et qu'il expliquait aux élèves que c'était la même chose. Mon bouquin de math parle d'ailleurs de "vecteurs parallèles".Parallèle et colinéaire sont très liés mais correspondent à deux objets différents (droites ou plans dans le premier cas, vecteurs dans le second) : je parierais donc plus sur une imprécision dans ton esprit qu'une évolution du langage.
J'ai aussi un peu de mal à comprendre comment on peut expliquer à des élèves la relation de Chasles si les vecteurs n'ont ni origine ni extrémité, mais sont toujours (des vecteurs) libres.
Oui une fonction linéaire + une constante de translation :zen:Linéaire et affine sont deux choses différentes (on en a déjà longuement parlé), mais très liées (une fonction affine est simplement une fonction linéaire + une constante) et là encore cela n'a pas évolué sur le dernier demi-siècle.
... Je suis pas si vieux que ça et je n'avais jamais entendu parler de fonction affine, par contre, la transformation appelée affinité, je sais ce que c'est et la transformation affine ( H + R + A [+ T]) aussi.
Elerinna a écrit:Un article sur la normeen espace
relate ce dilemme des voies imbriquées pour le taxi driver...
Maintenant que je sais que c'est aussi utilisé par ailleurs, et en particulier dans des domaines où je ne connais pas le premier mot, j'ai eu réponse à ma question.
Moi, à part les SIG, la 2.5D, la 3D et un peu de Gauss, j'y connais rien. Ah, j'oubliais la pluviométrie :doh: .
Mais je sais tout de même résoudre le problème du plus court chemin d'un point à un autre.
Merci tout de même.
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 9 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
