Salut
Arrêtes Rain' c'est très joli je connaissais pas ça !
ThSQ, je t'en donne 3 solutions différentes que j'ai trouvé sur le net, la deuxième je l'ai trouvé par hasard mais j'aime beaucoup ! on a fait la 1ère en cours ..
Soit

un sous-groupe d'ordre 6 de
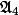
.

est distingué
car d'indice 2. 3 divisant l'ordre de

,

contient un élément d'ordre
3,

, et c'est un 3--cycle. Il y a 8 3--cycle dans

,
conjugués entre eux et le centralisateur de

dans

a 3 éléments, à savoir les puissances de

. Tout ça pour voir
que

possède
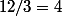
conjugués dans
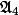
qui se
trouvent donc dans

. Il s'ensuit que

contient déjà 5 élements.
Reste dans

un autre élément

non conjugué à

, qui
ne peut être un 3--cycle (car sinon trop d'éléments dans

).

contient
donc un produit
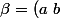(c\ d))
de deux transpositions à supports disjoints.
En prenant
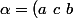\in\mathfrak{A}_4)
, on a
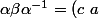(b\ d))
et cet élément doit appartenir à

qui aurait alors au moins 7 éléments...
Et la plus jolie :
On suppose que

possède un sous-groupe

d'ordre 6.

est d'indice 2 dans

, donc

est un sous-groupe distingué de

. On a donc

. Par suite pour tout

, on a

.
Soit

un élément d'ordre impair
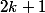
. Alors
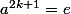
d'où
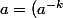^2\in G)
.
Le sous-groupe

contient donc tous les éléments d'ordre impair de

. Or il y en a 9 (8 3-cycles et l'élément neutre). Comme
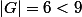
, on a là une contradiction.
Celle avec Sylow :
Si
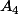
contenait un sous-groupe

d'ordre 6, celui-ci serait

soit cyclique d'ordre 6, mais
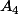
ne contient que des éléments d'ordre 2 ou 3

soit isomorphe à
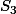
. Etant d'indice 2, H serait distingué et comme
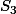
admet un sous-groupe caractéristique d'ordre 3 (c'est
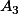
). Ce dernier serait donc distingué dans
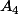
(caractéristique dans un distingué). Or les éléments d'ordre 3 de
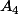
forment les 3-Sylow, qui sont au nombre de 4 conjugués entre eux, donc ne peut être distingué dans
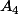
.
