Dénombrement et Combinatoire
36 messages
- Page 1 sur 2 - 1, 2
Dénombrement et Combinatoire
Bonjour, Vendredi je passe à un exposé oral en cour. Donc j'ai des infirmation (en noir) et je doit dire si elle sont vraie ou fausse et pourquoi.
1) Soient les ensembles E={0;1;2;3} et F={a,b} . Le nombre de parties de l’ensemble E est égal au nombre de mots de quatre lettres que l’on peut écrire avec les lettres de F.
Principe multiplicatif : élément peut se répéter et l’ordre compte.
Nous avons donc 4²=16
(a;b) (a;a;b) (b;b;b;a)
(b;a) (a;b,a) (b;b;a;b)
(b;a;a) (b;a;b;b)
(a;b;b;b)
(b;b;a)
(b;a;b) (a;a;a;b)
(a;b;b) (a;a;b;a)
(a;b;a;a)
(a;b;a;a)
2)Au basket-ball, un entraîneur décide de choisir cinq joueurs qu’il aligne sur le parquet parmi les 20 joueurs de son effectif.
Il a 20 !/15 ! possibilités s’il ne tient pas compte des postes occupés par les joueurs.
Faux :
Ce sont des éléments distincts et l’ordre ne compte pas donc c’est une combinaison.
20/(5)= 20!/(5!(20-5))= 20!/(5!15!)
=21x22x23x24x25/(1x2x3x4x5)
=53 130
Il y a donc 53 130 possibilités s’il ne tient pas compte des postes occupés par les joueurs.
3) Soit n un entier tel que n≥3 Alors (n-1) + ( n-1) =(n)
.........................................................................(n-2) .....( n-3)......(3)
Ici il n’y a que 3 parenthèse, mais elle sont longues :
Je sais pas si vous comprenez, mais pour faire court, lorsque vous voyez deux parenthèses l’une en dessous de l’autre, alors il n’y en a qu’une qui est longue. Bon je pense que c’est claire.
Bref ici je ne comprend pas vraiment.
Voila, pouvez vous m'aidai, je ne sais pas vraiment quoi dire. Pouvais vous me donner des conseilles pour ue je sois le plus claire à l'orale.
D'autre part je compte faire un powerpoint pour illustrer mais propos mais je ne sais pas comment écrire des fractions, ni des longues parenthèses. Pouvez vous m'aider.
1) Soient les ensembles E={0;1;2;3} et F={a,b} . Le nombre de parties de l’ensemble E est égal au nombre de mots de quatre lettres que l’on peut écrire avec les lettres de F.
Principe multiplicatif : élément peut se répéter et l’ordre compte.
Nous avons donc 4²=16
(a;b) (a;a;b) (b;b;b;a)
(b;a) (a;b,a) (b;b;a;b)
(b;a;a) (b;a;b;b)
(a;b;b;b)
(b;b;a)
(b;a;b) (a;a;a;b)
(a;b;b) (a;a;b;a)
(a;b;a;a)
(a;b;a;a)
2)Au basket-ball, un entraîneur décide de choisir cinq joueurs qu’il aligne sur le parquet parmi les 20 joueurs de son effectif.
Il a 20 !/15 ! possibilités s’il ne tient pas compte des postes occupés par les joueurs.
Faux :
Ce sont des éléments distincts et l’ordre ne compte pas donc c’est une combinaison.
20/(5)= 20!/(5!(20-5))= 20!/(5!15!)
=21x22x23x24x25/(1x2x3x4x5)
=53 130
Il y a donc 53 130 possibilités s’il ne tient pas compte des postes occupés par les joueurs.
3) Soit n un entier tel que n≥3 Alors (n-1) + ( n-1) =(n)
.........................................................................(n-2) .....( n-3)......(3)
Ici il n’y a que 3 parenthèse, mais elle sont longues :
Je sais pas si vous comprenez, mais pour faire court, lorsque vous voyez deux parenthèses l’une en dessous de l’autre, alors il n’y en a qu’une qui est longue. Bon je pense que c’est claire.
Bref ici je ne comprend pas vraiment.
Voila, pouvez vous m'aidai, je ne sais pas vraiment quoi dire. Pouvais vous me donner des conseilles pour ue je sois le plus claire à l'orale.
D'autre part je compte faire un powerpoint pour illustrer mais propos mais je ne sais pas comment écrire des fractions, ni des longues parenthèses. Pouvez vous m'aider.
Re: Dénombrement et Combinatoire
Bonjour,
Ton examen se passe en français ? Si oui, vérifie l'orthographe dans tes powerpoints.
Pour la question 3, il s'agit bien de nombres de combinaisons dans l'énoncé (n-2 parmi n-1, etc.) ?
Ton examen se passe en français ? Si oui, vérifie l'orthographe dans tes powerpoints.
Pour la question 3, il s'agit bien de nombres de combinaisons dans l'énoncé (n-2 parmi n-1, etc.) ?
Re: Dénombrement et Combinatoire
Bonsoir,
Il me semble que pour la dernière on va utiliser le triangle de Pascal.
SI on récrit "proprement" l'égalité proposée (à confirmer ou informer), cela devient :
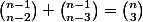
Le triangle de Pascal est
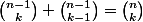
En utilisant cette formule, et en se souvenant que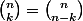 on sait répondre à la question.
on sait répondre à la question.
(Pour le triangle de PAscal, on peut le retenir ainsi : si x est le dernier élément de E qui en compte n, si E' est E sauf x, alors une partie de E contient x ou ne contient pas x: s'il ne contient pas x c'est une partie de E' à k éléments, s'il contient x c'est une partie de E' à k-1 élément que l'on réunit avec {x} : donc le nombre de parties de E à k éléments est égal au nombre de parties de E' à k éléments, plus le nombre de parties de E' à k-1 élément).
Il me semble que pour la dernière on va utiliser le triangle de Pascal.
SI on récrit "proprement" l'égalité proposée (à confirmer ou informer), cela devient :
Le triangle de Pascal est
En utilisant cette formule, et en se souvenant que
(Pour le triangle de PAscal, on peut le retenir ainsi : si x est le dernier élément de E qui en compte n, si E' est E sauf x, alors une partie de E contient x ou ne contient pas x: s'il ne contient pas x c'est une partie de E' à k éléments, s'il contient x c'est une partie de E' à k-1 élément que l'on réunit avec {x} : donc le nombre de parties de E à k éléments est égal au nombre de parties de E' à k éléments, plus le nombre de parties de E' à k-1 élément).
Modifié en dernier par hdci le 13 Jan 2021, 17:55, modifié 1 fois.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Dénombrement et Combinatoire
Jasminana a écrit:D'accord merci. Pour le 1) C'est bien un principe multiplicatif ?
Pour construire un mot de 4 lettres en les prenant dans un ensemble de k éléments, sans se soucier des éventuelles répétitions, c'est bien
Le nombre de parties d'un ensemble à n éléments est égal à
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Dénombrement et Combinatoire
D'accord merci. Pour le 1) C'est bien un principe multiplicatif ?
Donc c'est bien 4² si j'ai bien compris puisqu'il y a
Ceux à 1 lettre: (a) et (b)
Ceux avec 2x la lettre a : (a;a;b) (a;b;a) (b;a;a)
Ceux avec 2x la lettre b : (b;b;a) (b;a;a) (a;b;b)
Ceux avec 3 fois la lettre a: (a;a;a;b) (a;a;b;a) (a;b;a;a) (b:a:a:a)
Et enfin ceux avec 3 fois la lettre b (b:b:b:a) (b;b;a;b) (b;a;b;b) (a;b;b;b)
Je stress de devoir passer au tableau, surtout si je ne métrise pas complètement mon sujet. Est ce parfaitement cela ?
hdci a écrit:Jasminana a écrit:D'accord merci. Pour le 1) C'est bien un principe multiplicatif ?
Pour construire un mot de 4 lettres en les prenant dans un ensemble de k éléments, sans se soucier des éventuelles répétitions, c'est bienpuisqu'on a k choix pou la première, k choix pour la seconde (donc pour chacune des k possibilités de la première lettre, on a à nouveau k possibilités pour la seconde), etc.)
Le nombre de parties d'un ensemble à n éléments est égal à
Donc c'est bien 4² si j'ai bien compris puisqu'il y a
Ceux à 1 lettre: (a) et (b)
Ceux avec 2x la lettre a : (a;a;b) (a;b;a) (b;a;a)
Ceux avec 2x la lettre b : (b;b;a) (b;a;a) (a;b;b)
Ceux avec 3 fois la lettre a: (a;a;a;b) (a;a;b;a) (a;b;a;a) (b:a:a:a)
Et enfin ceux avec 3 fois la lettre b (b:b:b:a) (b;b;a;b) (b;a;b;b) (a;b;b;b)
Je stress de devoir passer au tableau, surtout si je ne métrise pas complètement mon sujet. Est ce parfaitement cela ?
Re: Dénombrement et Combinatoire
Bonjour, je vous propose de revoir les choses tranquillement pour le 1.
Pour le nombre de mots de 4 lettres, il s'agit bien d'un principe multiplicatif tel que vous le définissez mais ce n'est pas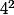 même si la valeur numérique est bonne. En fait il s'agit de
même si la valeur numérique est bonne. En fait il s'agit de 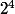
Pourquoi ?
Et bien chaque emplacement peut prendre 2 valeurs = a ou b et nous avons 4 emplacements donc 2x2x2x2 =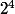
En pratique cela donne
(a,a,a,a) (a,a,a,b) (a,a,b,a) (a,b,a,a) (b,a,a,a) (a,a,b,b) (a,b,a,b) (b,a,a,b)
(b,a,b,a) (b,b,a,a) (a,b,b,a) (a,b,b,b) (b,a,b,b) (b,b,a,b) (b,b,b,a) (b,b,b,b)
Pour le nombre de parties d'un ensemble, le principe multiplicatif ne fonctionne plus car l'ordre ne compte pas mais comme le dit hdci, il y a toujours parties or ici n=4
parties or ici n=4
Quels sont les parties ?
{ensemble vide} => 1 choix avec 0 chiffre
{1} ou {2} ou {3} ou {0} => 4 choix avec 1 chiffre
{1;2} ou {1;3} ou {1;0} ou {2;3} ou {2;0} ou {3;0} => 6 choix avec 2 chiffres
{1;2;3} ou {1;2;0} ou {1;3;0} ou {2;3;0} => 4 choix avec 3 chiffres
{1;2;3;0} => 1 choix avec 4 chiffres
Au total, on retouve bien les 16 parties attendues
Pour le nombre de mots de 4 lettres, il s'agit bien d'un principe multiplicatif tel que vous le définissez mais ce n'est pas
Pourquoi ?
Et bien chaque emplacement peut prendre 2 valeurs = a ou b et nous avons 4 emplacements donc 2x2x2x2 =
En pratique cela donne
(a,a,a,a) (a,a,a,b) (a,a,b,a) (a,b,a,a) (b,a,a,a) (a,a,b,b) (a,b,a,b) (b,a,a,b)
(b,a,b,a) (b,b,a,a) (a,b,b,a) (a,b,b,b) (b,a,b,b) (b,b,a,b) (b,b,b,a) (b,b,b,b)
Pour le nombre de parties d'un ensemble, le principe multiplicatif ne fonctionne plus car l'ordre ne compte pas mais comme le dit hdci, il y a toujours
Quels sont les parties ?
{ensemble vide} => 1 choix avec 0 chiffre
{1} ou {2} ou {3} ou {0} => 4 choix avec 1 chiffre
{1;2} ou {1;3} ou {1;0} ou {2;3} ou {2;0} ou {3;0} => 6 choix avec 2 chiffres
{1;2;3} ou {1;2;0} ou {1;3;0} ou {2;3;0} => 4 choix avec 3 chiffres
{1;2;3;0} => 1 choix avec 4 chiffres
Au total, on retouve bien les 16 parties attendues
Modifié en dernier par Vassillia le 13 Jan 2021, 19:56, modifié 2 fois.
Re: Dénombrement et Combinatoire
Merci mille fois. J'ai parfaitement bien compris. C'était parfaitement claire pour moi. Merci.
Ensuite pour le deuxième, c'est un arrangement qui est utilisé, mais c'est faux.
Donc ça nous fait
20/(5)= 20!/(5!(20-5))
= 20!/(5!15!)
=21x22x23x24x25/(1x2x3x4x5)
=53 130
Ca me parait beaucoup non ?
Ensuite pour le deuxième, c'est un arrangement qui est utilisé, mais c'est faux.
Donc ça nous fait
20/(5)= 20!/(5!(20-5))
= 20!/(5!15!)
=21x22x23x24x25/(1x2x3x4x5)
=53 130
Ca me parait beaucoup non ?
Re: Dénombrement et Combinatoire
Nous sommes d'accord sur la formule qui est une combinaison de 5 parmi 20 mais votre calcul pose problème, 20! = 20x19x18x17x16x15x..., il n'est pas du tout logique que vous fassiez apparaitre du 21x22x23x24x25, je vous laisse reprendre votre calcul.
Re: Dénombrement et Combinatoire
Ah oui, moi même je ne comprend pas pourquoi j'ai fait ça!
Donc ça fait
20!/(5!)
=20!/(5!(20-5))
=16x17x81x19x20/(5!)
=15 504
Donc ça fait
20!/(5!)
=20!/(5!(20-5))
=16x17x81x19x20/(5!)
=15 504
Re: Dénombrement et Combinatoire
Au détail près de la faute de frappe qui a transformé le 18 en 81, c'est parfait 
Re: Dénombrement et Combinatoire
Merci beaucoup.
Pour le 3, j'ai pas vraiment compris:
Donc je sais qu'il faut utilisé le triangle de Pascale mais j'ai un peu de mal. J'ai lu l'explication juste en haut, mais c'est assez compliqué. Par ou je pourrait commencer?
Pour le 3, j'ai pas vraiment compris:
Donc je sais qu'il faut utilisé le triangle de Pascale mais j'ai un peu de mal. J'ai lu l'explication juste en haut, mais c'est assez compliqué. Par ou je pourrait commencer?
Re: Dénombrement et Combinatoire
Sans compter :
À un mot de quatre lettres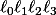 où les lettres
où les lettres 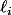 sont soit
sont soit  soit
soit  , on peut faire correspondre la partie de
, on peut faire correspondre la partie de 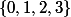 formée des
formée des  tels que
tels que 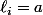 . On a ainsi une bijection entre l'ensemble des mots de quatre lettres et l'ensemble des parties de
. On a ainsi une bijection entre l'ensemble des mots de quatre lettres et l'ensemble des parties de 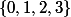 .
.
À un mot de quatre lettres
Re: Dénombrement et Combinatoire
Vassillia a écrit:Pour le 3, j'ai pas vraiment compris:
Quelle est la partie que vous trouvez compliqué : la formule, comment utiliser la formule, ou son explication ?
Si c'est la formule, et bien c'est juste une formule...
Pour l'explication de la formule, plus précisément : soit E un ensemble qui comporte 10 éléments (pour l'exemple) : les entiers de 1 à 10.
Si A est une partie de E de, disons 6 éléments, il y a deux possibilités :
- soit A contient le nombre 10 : auquel cas on peut dire que A est égal à une partie B contenant 5 éléments parmi 1 à 9, plus le 10
- Soit A ne contient pasle nombre 10, on peut donc dire qu'il contient 6 éléments parmi 9.
Dans le premier cas, B est un ensemble de 5 éléments pris dans un ensemble de 9 éléments (les nombres de 1 à 9) : il y a donc
Dans le second cas, A est un ensemble de 6 éléments pris dans un ensemble de 9 : il y a donc
Au final, le nombre d''ensembles A dans E, c'est la somme des deux nombres calculés précédemment, autrement dit
Et on généralise avec
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Dénombrement et Combinatoire
Mais... mais... hdci, j'avais parfaitement compris le 3, je pense qu'il y a une boulette dans les citations
Bon c'est pas grave du coup quitte à perdre toute crédibilité, je vais essayer de vulgariser un peu la jolie bijection de GaBuZoMeu (si je peux me permettre sinon je modifierai bien sur) car je doute fortement que Jasminana comprenne de quoi il retourne.
Disons qu'on s'intéresse à l’élément 0, soit il appartient à la partie que l'on regarde, soit il n'y appartient pas, il y a donc 2 possibilités.
Pareil pour l’élément 1, 2 et 3, ils ont chacun 2 possibilités : soit d'appartenir, soit de ne pas appartenir donc au final pour avoir toutes les parties, on multiplie toutes ses possibilités et on retrouve bien 2^4 parties différentes.
La bijection proposée est en fait une correspondance que l'on peut faire entre 2 questions :
l’élément i appartient-il à la partie ?
y a t'il la lettre "a" à la place numéro i ?
Bon c'est pas grave du coup quitte à perdre toute crédibilité, je vais essayer de vulgariser un peu la jolie bijection de GaBuZoMeu (si je peux me permettre sinon je modifierai bien sur) car je doute fortement que Jasminana comprenne de quoi il retourne.
Disons qu'on s'intéresse à l’élément 0, soit il appartient à la partie que l'on regarde, soit il n'y appartient pas, il y a donc 2 possibilités.
Pareil pour l’élément 1, 2 et 3, ils ont chacun 2 possibilités : soit d'appartenir, soit de ne pas appartenir donc au final pour avoir toutes les parties, on multiplie toutes ses possibilités et on retrouve bien 2^4 parties différentes.
La bijection proposée est en fait une correspondance que l'on peut faire entre 2 questions :
l’élément i appartient-il à la partie ?
y a t'il la lettre "a" à la place numéro i ?
Re: Dénombrement et Combinatoire
Bigre, comment se fait-il que la citation ait mélangé l'élément cité et l'auteur... ? Pourtant je sélectionne le texte et je clique sur "citation", il a dû y avoir un bug...
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Dénombrement et Combinatoire
Bonjour, voilà j'ai donc présenté mon sujet à ma classe, et je tenais à vous remercier pour votre aide. Grace à vous j'ai plutôt bien réussi mon exposé mais j'ai quand même rencontré quelque difficulté au 3eme énoncé. Je me demandais si ça dérangerais de m'aider sur cette partie s'il vous plaît, les évaluations arrivent très prochainement et je ne vous cache pas mon inquiétude.
Merci d'avance!
Merci d'avance!
Re: Dénombrement et Combinatoire
(n-1)+(n-1)=(n)
(n-2) (n-3) (3)
On utilise la formule pour calculer les factoriels : n!/( (n-k)! k! ) pour obtenir à la fin :
(n)
(3)
(n-1)!/ ( (n-1 - (n-2) ) ! (n-2)! ) + (n-1)! /( (n-1 -(n-3))! (n-3)! )
(n-1)! / ( ( n-1-n+2) ! (n-2)! + (n-1)! / ( (n-1-n+3)! (n-3)! )
Ensuite on met tous sur le même dénominateur: donc il faut que les dénominateurs des deux fractions soient les même:
Ici j'ai multiplié sur la 1er fraction par n en haut et en bas car (n-2)x n=(n-3)
Ensuite j'ai multiplié par (n-1) en haut et en bas de la 2eme fraction car (n-1-n+3) x (n-1)= (n-1-n+2)
(n-1)! x n / ( ( n-1-n+2)! (n-2)!x n ) + (n-1)! x( n-1) / ( (n-1-n+3)! (n-3)! x (n-1) )
Donc on a:
(n-1)! x n/ ( (n-1-n+2)! x n ) + (n-1)! (n-1) /( (n-1-n-2)! x n) )
(n-1)x n + (n-1) x n - (n-1) x (-1)/(n-1-n+2)! x n
Cela ne sert à rien de continué car je vois bien qu'il y a un problème. Pourrait-on m'aider.
(n-2) (n-3) (3)
On utilise la formule pour calculer les factoriels : n!/( (n-k)! k! ) pour obtenir à la fin :
(n)
(3)
(n-1)!/ ( (n-1 - (n-2) ) ! (n-2)! ) + (n-1)! /( (n-1 -(n-3))! (n-3)! )
(n-1)! / ( ( n-1-n+2) ! (n-2)! + (n-1)! / ( (n-1-n+3)! (n-3)! )
Ensuite on met tous sur le même dénominateur: donc il faut que les dénominateurs des deux fractions soient les même:
Ici j'ai multiplié sur la 1er fraction par n en haut et en bas car (n-2)x n=(n-3)
Ensuite j'ai multiplié par (n-1) en haut et en bas de la 2eme fraction car (n-1-n+3) x (n-1)= (n-1-n+2)
(n-1)! x n / ( ( n-1-n+2)! (n-2)!x n ) + (n-1)! x( n-1) / ( (n-1-n+3)! (n-3)! x (n-1) )
Donc on a:
(n-1)! x n/ ( (n-1-n+2)! x n ) + (n-1)! (n-1) /( (n-1-n-2)! x n) )
(n-1)x n + (n-1) x n - (n-1) x (-1)/(n-1-n+2)! x n
Cela ne sert à rien de continué car je vois bien qu'il y a un problème. Pourrait-on m'aider.
36 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
