Degre 5
25 messages
- Page 1 sur 2 - 1, 2
degre 5
on a:
-61086689/30222244158804*b^4-15469445/30222244158804*b^3+1217816335/30222244158804*b^2+308396855/30222244158804*b-6030571225/30222244158804 = 0
puis:
x^2+b= 0
x donne 4 solutions de l'équation x^5-10*x+5= 0
mais j'ai bien peur que ce ne sont que des approximations
-61086689/30222244158804*b^4-15469445/30222244158804*b^3+1217816335/30222244158804*b^2+308396855/30222244158804*b-6030571225/30222244158804 = 0
puis:
x^2+b= 0
x donne 4 solutions de l'équation x^5-10*x+5= 0
mais j'ai bien peur que ce ne sont que des approximations
Re: degre 5
Bonjour
Vous voyez bien que les solutions (pour b) de
-61086689/30222244158804*b^4-15469445/30222244158804*b^3+1217816335/30222244158804*b^2+308396855/30222244158804*b-6030571225/30222244158804 = 0
sont strictement les mêmes que les solutions pour b de
-61086689*b^4-15469445*b^3+1217816335*b^2+308396855*b-6030571225= 0
et sont strictement les mêmes que celles de
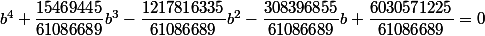
Ensuite votre équation du quatrième degré donne deux solutions réelles positives (je n'ai pas calculé algébriquement cela mais ce n'est pas important ici) donc du coup avec ce que vous dites on doit vérifier que (par exemple)
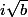 serait (selon vos dires) une solution de votre équation du cinquième degré
serait (selon vos dires) une solution de votre équation du cinquième degré
avec un b solution de votre équation du quatrième degré (et on va prendre une des racines réelles)
j'ai pris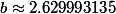
et là je n'obtiens pas du tout cela
Vous voyez bien que les solutions (pour b) de
-61086689/30222244158804*b^4-15469445/30222244158804*b^3+1217816335/30222244158804*b^2+308396855/30222244158804*b-6030571225/30222244158804 = 0
sont strictement les mêmes que les solutions pour b de
-61086689*b^4-15469445*b^3+1217816335*b^2+308396855*b-6030571225= 0
et sont strictement les mêmes que celles de
Ensuite votre équation du quatrième degré donne deux solutions réelles positives (je n'ai pas calculé algébriquement cela mais ce n'est pas important ici) donc du coup avec ce que vous dites on doit vérifier que (par exemple)
avec un b solution de votre équation du quatrième degré (et on va prendre une des racines réelles)
j'ai pris
et là je n'obtiens pas du tout cela
Re: degre 5
ok alors dans ce cas vous vous trompez
ce ne sont pas quatre solutions mais seulement deux
la premiere est la racine carrée de la racine réelle inférieure de votre poly de degré 4
la deuxième est le négatif de la racine carrée de la racine réelle supérieure de votre poly de degré 4
J'ai fait ça sans aller voir algébriquement qq chose
ce ne sont pas quatre solutions mais seulement deux
la premiere est la racine carrée de la racine réelle inférieure de votre poly de degré 4
la deuxième est le négatif de la racine carrée de la racine réelle supérieure de votre poly de degré 4
J'ai fait ça sans aller voir algébriquement qq chose
Re: degre 5
le negatif des deux racines carrees des solutions complexe du polynome de degre 4 sont aussi solutions de l'equation de degré 5
Re: degre 5
Re Edit erreur dans le titre de la cinquième partie : quatre poly de degré deux (pas huit) et donc huit racines à vérifier bon je retourne au taff (à ce soir pour la suite)
Edit : je reviens dans la soirée plutôt là je bosse et après je vais dormir un peu mais bon moi deux trois heures ça me suffit et même des fois rien que le fait de faire semblant de me coucher ça me fait croire que j'ai dormi
(faut juste savoir mentir astucieusement à soi même et si on s'y prend bien ça marche)
ok
bah c'était pas clair car tel que vous avez écrit les poly il y a quatre polynômes du second degré et éventuellement identiques pour certains (on ne parle pas de racine carré d'un nombre complexe mais de racines de ces polynômes là)
mais tel que vous parlez de cela on dirait que vous ne les voyez pas car vous parlez de quatre racines
mais ces quatre racines sont des racines du poly de degré 4
et là on a 4*2=8 racines à considérer (éventuellement multiples) et voir lesquelles de celles-ci seraient des racines de votre poly de degré cinq
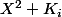 avec
avec 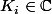 est une racine du poly de degré quatre
est une racine du poly de degré quatre
Sommaire
Introduction
Première partie: Écriture de la réduite du polynôme unitaire du quatrième degré
Deuxième partie: Écriture de la solvante de la réduite du polynôme unitaire du quatrième degré
Troisième partie: Racines de la solvante de la réduite du polynôme unitaire du quatrième degré
pause clope juste après l'avertissement donné dans cette partie là (retour vers midi)
Quatrième partie: Racines du polynôme unitaire du quatrième degré
Cinquième partie: Racines des quatre polynômes du second degré
Conclusion
introduction
Je m'en étais tenu jusque-là aux racines réelles données par ma machine de fabrication soviétique (Elektronika MK-61 de 1983) et confisquée par décision de justice locale puis revendue (légalement je précise) par la milice (locale aussi) contre trois cartouches de Marlboro que j'ai par la suite recyclées en suivant discrètement les miliciens de près car une clope fumée se recycle avec son mégot dans lequel il reste toujours un peu de tabac
...et il faut que vous comprenniez qu'avec ce qui est écrit dans votre premier post il y a au total huit racines de polynômes
4*2=8 et certaines seraient des racines du polynôme de degré cinq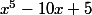
et comme vous parlez de quatre racines il faut repartir avec le bon vocabulaire
À ce propos dans ce qui va suivre on ne parlera pas de racine carrée de nombres complexes
il s'agira ici de parler de racines de polynomes du second degré à coefficients complexes de la forme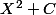 avec
avec 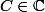
Donc allons-y et recherchons les quatres racines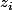 avec
avec 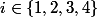 du polynôme du quatrième degré
du polynôme du quatrième degré
Première partie: Écriture de la réduite du polynôme unitaire du quatrième degré
Le polynôme unitaire est
:= z^4+\dfrac {15469445}{61086689}z^3-\dfrac {1217816335}{61086689}z^2-\dfrac {308396855}{61086689}z+\dfrac {6030571225}{61086689})
Entre nous c'est une mauvaise idée d'utiliser la lettre b pour écrire les racines
Je vais écrire à ma manière les lettres car sinon ça va être le bordel
Je vais utiliser la lettre b pour autre chose et poser
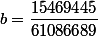
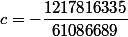
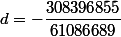
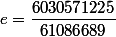
donc remplacez votre lettre b par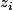 avec
avec 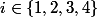
et on va avoir les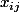 avec
avec 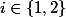 et
et 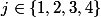 comme elles sont décrites ci-dessous
comme elles sont décrites ci-dessous
On doit rechercher les deux racines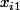 du polynôme
du polynôme 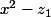
les deux racines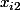 du polynôme
du polynôme 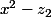
les deux racines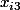 du polynôme
du polynôme 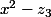
les deux racines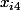 du polynôme
du polynôme 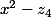
et voir lequelles de ces huit racines lesquelles seraient racines de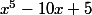
:=w^4+pw^2+qw+r) la réduite de
la réduite de )
par translation selon les relations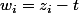 et
et 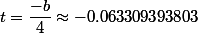 alors
alors
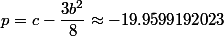
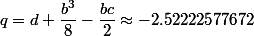
il n'y a pas certains cas particuliers (que je ne précise pas) on passe donc à la suite
Deuxième partie: Écriture de la solvante de la réduite du polynôme unitaire du quatrième degré
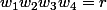
On va considérer les valeurs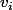 pour lesquelles on vérifie
pour lesquelles on vérifie
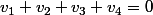
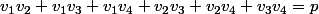
^2=q^2)
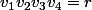
alors il existe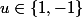 tel que
tel que 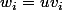
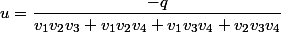
On considère la solvante de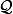 est définie par
est définie par
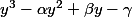
on a (je passe les détails)
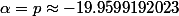
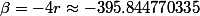
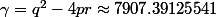
Troisième partie: Racines de la solvante de la réduite du polynôme unitaire du quatrième degré
ATTENTION: Dans cette troisième partie on va faire un aparté pour distinguer les lettres utilisées pour la résolution de cette solvante
Les lettres de l'alphabet qui seront utilisées dans cette partie ne concernent que la résolution de cette solvante
pause clope
Edit : je reviens dans la soirée plutôt là je bosse et après je vais dormir un peu mais bon moi deux trois heures ça me suffit et même des fois rien que le fait de faire semblant de me coucher ça me fait croire que j'ai dormi
(faut juste savoir mentir astucieusement à soi même et si on s'y prend bien ça marche)
ok
bah c'était pas clair car tel que vous avez écrit les poly il y a quatre polynômes du second degré et éventuellement identiques pour certains (on ne parle pas de racine carré d'un nombre complexe mais de racines de ces polynômes là)
mais tel que vous parlez de cela on dirait que vous ne les voyez pas car vous parlez de quatre racines
mais ces quatre racines sont des racines du poly de degré 4
et là on a 4*2=8 racines à considérer (éventuellement multiples) et voir lesquelles de celles-ci seraient des racines de votre poly de degré cinq
Sommaire
Introduction
Première partie: Écriture de la réduite du polynôme unitaire du quatrième degré
Deuxième partie: Écriture de la solvante de la réduite du polynôme unitaire du quatrième degré
Troisième partie: Racines de la solvante de la réduite du polynôme unitaire du quatrième degré
pause clope juste après l'avertissement donné dans cette partie là (retour vers midi)
Quatrième partie: Racines du polynôme unitaire du quatrième degré
Cinquième partie: Racines des quatre polynômes du second degré
Conclusion
introduction
Je m'en étais tenu jusque-là aux racines réelles données par ma machine de fabrication soviétique (Elektronika MK-61 de 1983) et confisquée par décision de justice locale puis revendue (légalement je précise) par la milice (locale aussi) contre trois cartouches de Marlboro que j'ai par la suite recyclées en suivant discrètement les miliciens de près car une clope fumée se recycle avec son mégot dans lequel il reste toujours un peu de tabac
...et il faut que vous comprenniez qu'avec ce qui est écrit dans votre premier post il y a au total huit racines de polynômes
4*2=8 et certaines seraient des racines du polynôme de degré cinq
et comme vous parlez de quatre racines il faut repartir avec le bon vocabulaire
À ce propos dans ce qui va suivre on ne parlera pas de racine carrée de nombres complexes
il s'agira ici de parler de racines de polynomes du second degré à coefficients complexes de la forme
Donc allons-y et recherchons les quatres racines
Première partie: Écriture de la réduite du polynôme unitaire du quatrième degré
Le polynôme unitaire est
Entre nous c'est une mauvaise idée d'utiliser la lettre b pour écrire les racines
Je vais écrire à ma manière les lettres car sinon ça va être le bordel
Je vais utiliser la lettre b pour autre chose et poser
donc remplacez votre lettre b par
et on va avoir les
On doit rechercher les deux racines
les deux racines
les deux racines
les deux racines
et voir lequelles de ces huit racines lesquelles seraient racines de
par translation selon les relations
il n'y a pas certains cas particuliers (que je ne précise pas) on passe donc à la suite
Deuxième partie: Écriture de la solvante de la réduite du polynôme unitaire du quatrième degré
On va considérer les valeurs
alors il existe
On considère la solvante de
on a (je passe les détails)
Troisième partie: Racines de la solvante de la réduite du polynôme unitaire du quatrième degré
ATTENTION: Dans cette troisième partie on va faire un aparté pour distinguer les lettres utilisées pour la résolution de cette solvante
Les lettres de l'alphabet qui seront utilisées dans cette partie ne concernent que la résolution de cette solvante
pause clope
Re: degre 5
Je reviens dans la nuit camarade Alphax pour la suite de l'expression des racines
Je suis rentré du taff là et j'ai dormi deux heures environ et c'était génial : j'ai rêvé (en fait je suis vite parti en sommeil profond et vite revenu et du coup deux heures valent un vrai sommeil là pour le coup ) et bon là je suis en transe mais pas à cause de moi (oui je sais c'est toujours la faute aux autres mais bon là je pense avoir une bonne excuse) , c'est Monsieur Laurent Henninger, historien, chargé d'études à l'Irsem (Institut de recherche stratégique de l'école militaire) avec sa conférence qui m'a fait partir en transe oui car avec les bon mots je pars en transe assez facilement
Donc je reviens cette nuit
Je suis rentré du taff là et j'ai dormi deux heures environ et c'était génial : j'ai rêvé (en fait je suis vite parti en sommeil profond et vite revenu et du coup deux heures valent un vrai sommeil là pour le coup ) et bon là je suis en transe mais pas à cause de moi (oui je sais c'est toujours la faute aux autres mais bon là je pense avoir une bonne excuse) , c'est Monsieur Laurent Henninger, historien, chargé d'études à l'Irsem (Institut de recherche stratégique de l'école militaire) avec sa conférence qui m'a fait partir en transe oui car avec les bon mots je pars en transe assez facilement
Donc je reviens cette nuit
Re: degre 5
Toujours à poursuivre la même chimère, alphax ?
Voir https://www.maths-forum.com/post1398365.html#p1398365
Voir https://www.maths-forum.com/post1398365.html#p1398365
Re: degre 5
Merci GabuZoMeu
C'est clair que des approximations même infime à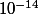 près ne rendent pas une égalité
près ne rendent pas une égalité
Ceci dit ici je vais lui donner ses racines du poly de degré quatre (dans la nuit donc) avec les expressions et après ce sera à lui de croire (ou pas) que ces expressions du genre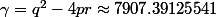 qui se suivent ensuite avec des
qui se suivent ensuite avec des  sont des égalités
sont des égalités
mais pour consolider sa croyance au moins qu'il sache que les deux symboles et
et  ne sont pas identiques
ne sont pas identiques
Vous avez bien fait d'intervenir GaBuZoMeu (je rappellerai cela dans ma conclusion)
Bon je retourne à ma transe (à plus tard Alphax)
C'est clair que des approximations même infime à
Ceci dit ici je vais lui donner ses racines du poly de degré quatre (dans la nuit donc) avec les expressions et après ce sera à lui de croire (ou pas) que ces expressions du genre
mais pour consolider sa croyance au moins qu'il sache que les deux symboles
Vous avez bien fait d'intervenir GaBuZoMeu (je rappellerai cela dans ma conclusion)
Bon je retourne à ma transe (à plus tard Alphax)
Re: degre 5
GaBuZoMeu a écrit:Toujours à poursuivre la même chimère, alphax ?
possible aussi qu'on parle tout seul (disons que ça serait rigolo)
Bon là la troisième partie (les racines de la solvante)
ça va aller plus vite à partir de là
ATTENTION(rappel à copier coller dans la conclusion):
Comme le fait justement remarquer en résumé GaBuZoMeu dans le lien qu'il a donné
Écrire
Troisième partie: Racines de la solvante de la réduite du polynôme unitaire du quatrième degré
ATTENTION: Dans cette troisième partie on va faire un aparté pour distinguer les lettres utilisées pour la résolution de cette solvante
Les lettres de l'alphabet qui seront utilisées dans cette partie ne concernent que la résolution de cette solvante
On considère la solvante de
on a
Je passe les détails car on verra la relation entre les
Donc ici on va se donner les lettres de l'alphabet qui ne seront valable que pour cette troisième partie
On va poser
On va donc oublier la signification des lettres de l'alphabet des précédentes parties et y compris
Pour un programmeur cette troisième partie se présente comme une fonction avec
On n'a pas de cas particulier (inutile de le décrire) donc on continue
On n'a pas des cas particuliers (inutile de les décrire) donc on continue
On pose
alors
On obtient
À présent on va rechercher les racines de
Bon au lieu d'utiliser la traditionnelle racine cubique
On peut tout simplement considérer que
et comme
pour
pour
et ici vu que
avec
ce sont les trois racines de ce polynôme là et avec elles on va poser
Quatrième partie: Racines du polynôme unitaire du quatrième degré
bon à partir de là on reprend les lettres qu'on avait utilisé dans la première et deuxième partie
la solvante de
on a
pause clope (il ne reste plus beaucoup à faire, on va dire plus que deux posts au max, je reviens dans la journée ou la soirée enfin bref dans les 24h en comptant large)
Re: degre 5
Un petit coup de SageMath :
On demande les racines de P :
[(-1.885960795979260?, 1),
(-1.621725357322074?, 1),
(1.621725357322074?, 1),
(1.885960795979260?, 1),
(-0.1194958603985575? - 1.798421162446029?*I, 1),
(-0.1194958603985575? + 1.798421162446029?*I, 1),
(0.1194958603985575? - 1.798421162446029?*I, 1),
(0.1194958603985575? + 1.798421162446029?*I, 1)]
Celles de Q :
[(-1.885960795984088?, 1),
(0.503227158966588?, 1),
(1.621725357850640?, 1),
(-0.11949586041656978? - 1.798421162453291?*I, 1),
(-0.11949586041656978? + 1.798421162453291?*I, 1)]
Aucune racine commune bien sûr, seulement des approximations.
On peut vérifier que les deux polynômes sont premiers entre eux, avec en prime les coefficients d'une identité de Bézout.
(1,
-52888927277907/25*x^4 + 612000444215781/25*x^3 - 362666929905648/5*x^2 + 423111418223256/5*x - 136000098714618/5,
-427606823/100*x^7 + 4948021809/100*x^6 - 590763659/4*x^5 + 3671459593/20*x^4 - 992364539/20*x^3 - 4269342633/10*x^2 + 6030571227/5*x - 10855028203/10)
- Code: Tout sélectionner
R.<x>=PolynomialRing(QQ,x)
b=x^2
P=-61086689/30222244158804*b^4-15469445/30222244158804*b^3\
+1217816335/30222244158804*b^2+308396855/30222244158804*b\
-6030571225/30222244158804
Q=x^5-10*x+5
On demande les racines de P :
- Code: Tout sélectionner
P.roots(QQbar)
[(-1.885960795979260?, 1),
(-1.621725357322074?, 1),
(1.621725357322074?, 1),
(1.885960795979260?, 1),
(-0.1194958603985575? - 1.798421162446029?*I, 1),
(-0.1194958603985575? + 1.798421162446029?*I, 1),
(0.1194958603985575? - 1.798421162446029?*I, 1),
(0.1194958603985575? + 1.798421162446029?*I, 1)]
Celles de Q :
- Code: Tout sélectionner
Q.roots(QQbar)
[(-1.885960795984088?, 1),
(0.503227158966588?, 1),
(1.621725357850640?, 1),
(-0.11949586041656978? - 1.798421162453291?*I, 1),
(-0.11949586041656978? + 1.798421162453291?*I, 1)]
Aucune racine commune bien sûr, seulement des approximations.
On peut vérifier que les deux polynômes sont premiers entre eux, avec en prime les coefficients d'une identité de Bézout.
- Code: Tout sélectionner
P.xgcd(Q)
(1,
-52888927277907/25*x^4 + 612000444215781/25*x^3 - 362666929905648/5*x^2 + 423111418223256/5*x - 136000098714618/5,
-427606823/100*x^7 + 4948021809/100*x^6 - 590763659/4*x^5 + 3671459593/20*x^4 - 992364539/20*x^3 - 4269342633/10*x^2 + 6030571227/5*x - 10855028203/10)
Re: degre 5
Bonjour GaBuZoMeu
Je vais quand même terminer (je me doute bien qu'Alphax est parti)
À venir donc la quatrième partie et la cinquième partie et la conclusion
Je pense avoir posté ça pour 07:00 heures demain (là je suis en train d'écouter du punk et je ne pense pas qu'il soit très pressé non plus)
Au final on va se retrouver avec des approximations de zéro en appliquant les racines obtenues des autres polynômes avec son polynôme du cinquième degré
Je vais quand même terminer (je me doute bien qu'Alphax est parti)
À venir donc la quatrième partie et la cinquième partie et la conclusion
Je pense avoir posté ça pour 07:00 heures demain (là je suis en train d'écouter du punk et je ne pense pas qu'il soit très pressé non plus)
Au final on va se retrouver avec des approximations de zéro en appliquant les racines obtenues des autres polynômes avec son polynôme du cinquième degré
Re: degre 5
mémo:
La valeur de t c'est bien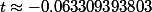
c'est la lettre t utilisée dans la première partie et non celle utilisée de la troisième partie
Les lettres utilisées pour la troisième partie sont uniquement valables que dans cette partie là
------------
Alphax là la quatrième partie
Quatrième partie: Racines du polynôme unitaire du quatrième degré
bon à partir de là on reprend les lettres qu'on avait utilisé dans la première et deuxième partie
la solvante de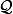 est définie par
est définie par
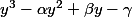
on a
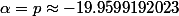
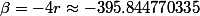
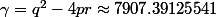
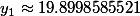 première racine de la solvante
première racine de la solvante
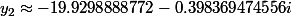 deuxième racine de la solvante
deuxième racine de la solvante
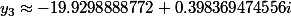 troisième racine de la solvante
troisième racine de la solvante
À présent on recherche les valeurs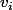 lesquelles vérifient (voir précédemment les autres relations dans la deuxième partie)
lesquelles vérifient (voir précédemment les autres relations dans la deuxième partie)
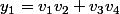
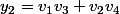
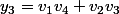
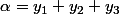
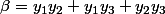
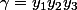
On va appliquer sur des couples de nombres réels ou complexes la relation suivante
somme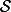 et produit
et produit 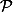 de couples de nombres réels ou complexes
de couples de nombres réels ou complexes
et qui sont les racines des polynômes de type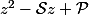
où à ce propos la réduite d'un polynôme du second degré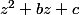 s'écrit
s'écrit 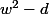 avec la relation d'une translation
avec la relation d'une translation 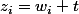
où pour un nombre complexe non nul d'argument principal
d'argument principal  les racines de cette réduite seront
les racines de cette réduite seront
+Im^2\left(d\right)}\right)^{\dfrac {1}{2}}\left(cos\left(\dfrac {\theta +2\pi k}{2}\right)+isin\left(\dfrac {\theta +2\pi k}{2}\right)\right))
avec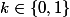
Fin de l'à-propos
1.En posant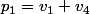 et
et 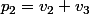
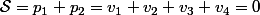
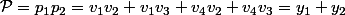
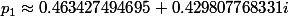
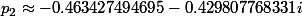
2.En posant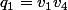 et
et 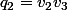
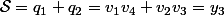
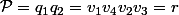
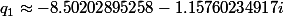
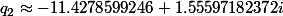
3.En posant
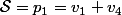
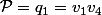
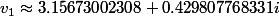
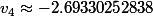
4.En posant
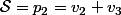
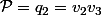
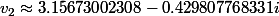
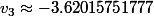
alors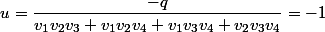
tout rond là pour le coup et c'est normal car ceci ne peut être une approximation
même si la machine va renvoyer une partie imaginaire de zéro à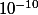 près
près
La raison étant algébrique
comme c'est dit plus haut on a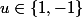
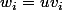 alors
alors
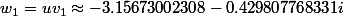
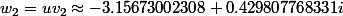
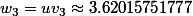
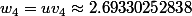
 sont les racines du polynôme de degré 4
sont les racines du polynôme de degré 4
que dans votre premier post écrivez par la lettre b
première racine du polynôme de degré 4 avec son approximation
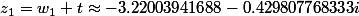
deuxième racine du polynôme de degré 4 avec son approximation
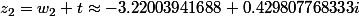
troisième racine du polynôme de degré 4 avec son approximation
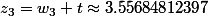
quatrième racine du polynôme de degré 4 avec son approximation
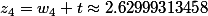
Pause clope
À venir la cinquième partie puis la conclusion
(tout à l'heure)
La valeur de t c'est bien
c'est la lettre t utilisée dans la première partie et non celle utilisée de la troisième partie
Les lettres utilisées pour la troisième partie sont uniquement valables que dans cette partie là
------------
Alphax là la quatrième partie
Quatrième partie: Racines du polynôme unitaire du quatrième degré
bon à partir de là on reprend les lettres qu'on avait utilisé dans la première et deuxième partie
la solvante de
on a
À présent on recherche les valeurs
On va appliquer sur des couples de nombres réels ou complexes la relation suivante
somme
et qui sont les racines des polynômes de type
où à ce propos la réduite d'un polynôme du second degré
où pour un nombre complexe non nul
avec
Fin de l'à-propos
1.En posant
2.En posant
3.En posant
4.En posant
alors
tout rond là pour le coup et c'est normal car ceci ne peut être une approximation
même si la machine va renvoyer une partie imaginaire de zéro à
La raison étant algébrique
comme c'est dit plus haut on a
que dans votre premier post écrivez par la lettre b
première racine du polynôme de degré 4 avec son approximation
deuxième racine du polynôme de degré 4 avec son approximation
troisième racine du polynôme de degré 4 avec son approximation
quatrième racine du polynôme de degré 4 avec son approximation
Pause clope
À venir la cinquième partie puis la conclusion
(tout à l'heure)
Re: degre 5
Bonjour,
Copier-coller de l'équation en b dans ma calculette favorite ...
b = 2,62999313458
b = 3,55684812397
b = -3,22003941688 - 0,42980776833.i
b = -3,22003941688 + 0,42980776833.i
*************
x² - b = 0
x² - 2,62999313458 = 0 --> x = +/- 1,62172535732
x² - 3,55684812397 = 0 --> x = +/- 1,88596079598
x² - (-3,22003941688 + 0,42980776833.i) = 0 ---> x = +/- (0,119495860398 + 1,79842116245.i)
x² - (-3,22003941688 - 0,42980776833.i) = 0 ---> x = +/- (0,119495860398 - 1,79842116245.i)
*************
Et les 5 solutions de x^5 - 10x + 5 = 0 sont :
1,62172535785
-1,88596079598
-0,119495860416 + 1,79842116245.i
-0,119495860416 - 1,79842116245.i
0,503227158967
Tout cela, aux arrondis de la calculette près.... évidemment.

Copier-coller de l'équation en b dans ma calculette favorite ...
b = 2,62999313458
b = 3,55684812397
b = -3,22003941688 - 0,42980776833.i
b = -3,22003941688 + 0,42980776833.i
*************
x² - b = 0
x² - 2,62999313458 = 0 --> x = +/- 1,62172535732
x² - 3,55684812397 = 0 --> x = +/- 1,88596079598
x² - (-3,22003941688 + 0,42980776833.i) = 0 ---> x = +/- (0,119495860398 + 1,79842116245.i)
x² - (-3,22003941688 - 0,42980776833.i) = 0 ---> x = +/- (0,119495860398 - 1,79842116245.i)
*************
Et les 5 solutions de x^5 - 10x + 5 = 0 sont :
1,62172535785
-1,88596079598
-0,119495860416 + 1,79842116245.i
-0,119495860416 - 1,79842116245.i
0,503227158967
Tout cela, aux arrondis de la calculette près.... évidemment.
Re: degre 5
Black Jack a écrit:
Copier-coller de l'équation en b dans ma calculette favorite ...
b = 2,62999313458
b = 3,55684812397
b = -3,22003941688 - 0,42980776833.i
b = -3,22003941688 + 0,42980776833.i
Bonjour Black Jack
on a pareil (c'était la quatrième partie)
ce soir la cinquième partie et normalement ça va coller avec les huit de GaBuZoMeu
PS: j'ai corrigé la coquille pour u
donc c'était u=-1
Re: degre 5
Remarque :
On voit que la calculette de Black Jack ne permet pas de faire la différence entre le -1,88596079598 racine du polynôme du huitième degré et le -1,88596079598 racine de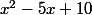 .
.
SageMath permet de faire la différence, et en fait il a une représentation exacte des deux nombres comme nombres algébriques réels : sous forme du polynôme minimal sur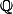 du nombre algébrique, et d'un intervalle qui l'isole des autres racines de ce polynôme.Ce qui fait que même si toutes les décimales indiquées par SageMath étaient les mêmes, il répondrait "non" à la question de savoir si les deux nombres sont égaux.
du nombre algébrique, et d'un intervalle qui l'isole des autres racines de ce polynôme.Ce qui fait que même si toutes les décimales indiquées par SageMath étaient les mêmes, il répondrait "non" à la question de savoir si les deux nombres sont égaux.
On voit que la calculette de Black Jack ne permet pas de faire la différence entre le -1,88596079598 racine du polynôme du huitième degré et le -1,88596079598 racine de
SageMath permet de faire la différence, et en fait il a une représentation exacte des deux nombres comme nombres algébriques réels : sous forme du polynôme minimal sur
Re: degre 5
Merci GaBuZoMeu
non je ne connais pas
J'ai trouvé un pdf en français sur Sage Math
http://dl.lateralis.org/public/sagebook/sagebook-web-20130530.pdf
non je ne connais pas
J'ai trouvé un pdf en français sur Sage Math
http://dl.lateralis.org/public/sagebook/sagebook-web-20130530.pdf
25 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 1 invité
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
