Caractérisation d'une meilleure approximation

par **rocentin** » 25 Mai 2007, 11:53

Je cherche à démontrer (sans réussite) les 2 résultats suivants:

le rationnel p/q est une meilleur approximation de x => |x - p/q | p/q est une réduite de x (ou un meilleur approximation de x, c'est équivalent!) (d'aprés le dévellopement en fraction continue...)

à titre informatif, je m'appuie sur la définition suivante:
un rationnel p/q est dit meilleur approximation de x ssi:
pour tout p'/q' avec 0<q'<ou=q, |qx - p|<|q'x - p'|.

Je me suis attaché à une démonstration par l'absurbe pour le premier point que je n'arrive pas à aboutir... (il s'agit de trouver p'/q' tel que |q'x - p'|<|qx - p|...ce qui contredirait la prémice!).
Pour ce qui est du second ennoncé il parait assez proche du premier mais ne se laisse pas non plus faire trés facilement.
Merci d'avance de l'aide que vous pourrez m'apporter en m'indiquant vos idées ou d'éventuelles sources d'informations pouvant me mettre sur la piste.

par **Lierre Aeripz** » 25 Mai 2007, 20:34

Pour le premier point.

Il s'agit de montrer une résultat assez classique. On pose

et

.
Montrons que

.
Alors

, ie

.
Avec

et

, on a bien l'inégalité recherchée :

.

NB : p et q ne sont pas donnés, on les a exhibés.

par **cesar** » 25 Mai 2007, 20:36

excusez mon ignorance, mais :
- x est il reel ou rationel ?
- quel est la definition de "meilleure approximation de x" ?? :briques:

par **rocentin** » 26 Mai 2007, 09:07

pour x réel on définit ainsi une meilleur approximation de x:

un rationnel p/q est dit meilleur approximation de x ssi:
pour tout p'/q' avec 0<q'<ou=q, |qx - p|<|q'x - p'|.

x peut être rationnel (par exmple 2/3 est une meilleur approximation de 0.7) ou irationnel (comme le nombre d'or ou encore Pie).

MERCI BEAUCOUP à Lierre Aeripz pour sa précieuse aide :happy2: .
Je me permet de vous soummettre un autre petit probléme concernant les fractions continues, il s'agit de démontrer que:

[a1,a2,a3...,an-1,y]=(yPn-1+Pn-2)/(yQn-1+Qn-2)

C'est à dire faire le lien entre les réduites [a1,a2,a3..,an] et Pn/Qn définit par la récurrence d'ordre 2...

par **Lierre Aeripz** » 26 Mai 2007, 10:32

Je n'ai pas bien compris le problème que tu me propose.

par **cesar** » 26 Mai 2007, 10:35

rocentin a écrit:pour x réel on définit ainsi une meilleur approximation de x:

un rationnel p/q est dit meilleur approximation de x ssi:
pour tout p'/q' avec 0<q'<ou=q, |qx - p|<|q'x - p'|.

x peut être rationnel (par exmple 2/3 est une meilleur approximation de 0.7) ou irationnel (comme le nombre d'or ou encore Pie).

.

OK, merci :we:

voir
http://fr.wikipedia.org/wiki/Fraction_continue
cela eclaircira un peu le nouveau probleme, mais l'enoncé n'est pas clair...

par **rocentin** » 26 Mai 2007, 10:40

sachant ce qu'est la meilleure approximation d'un réel (voir messages précedent),je veux montrer ceci:

soit x un réel,
soit p/q une meilleure approximation de x donnée (vérifiant donc que pour tout p'/q' avec 0<q'<ou=q, |qx - p|<|q'x - p'|),

je veux montrer l'inégalité |qx - p |< 1/q².

Il me semble que, si la considération des Cj et Ij dans la démonstration proposé est interessante (j'éssaie de l'exploiter actuellement), la démonstration proposé précédemment ne répond pas tout à fait au probleme!

je reste à l'écoute de vos propositions! :we:

par **rocentin** » 26 Mai 2007, 10:45

cesar a écrit:http://fr.wikipedia.org/wiki/Fraction_continue
cela eclaircira un peu le nouveau probleme, mais l'enoncé n'est pas clair...

L'article est effectiviement trés complet est interessant mais ne propose pas vraiment de démonstration, je souhaite dans ma démarche ne m'appuyer que sur des résultats que je puisse justifier.
Cependant le sérieux de cet article (même s'il apporte plus de questions que de réponses)est à souligner!

par **Lierre Aeripz** » 26 Mai 2007, 11:17

Du résultat que dont ej t'ai expliqué la démonstration on retrouve immédiatement ce que tu cherche, par le raisonnement par l'absurde que tu proposais dans ton premier message.

Soit

tel que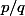

soit une meilleure approximation de

.
Supposons que

.

Par le résultat, il existe

tel que

. Donc

. Absurde car

et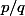

est une meilleure approximation de

.

Donc

par **rocentin** » 26 Mai 2007, 12:20

Mais bon sang mais c'est bien sur!!!
Merci pour cette derniére précision (qui était dans mon exprit le chainon manquant!!),j'avais sans doute un peu trop la tête dans mon probléme...
le voilà maintenant résolu!

Il reste cependant pour les ammateurs le deuxième énoncé:
|x - p/q| p/q est une réduite de x

Je vais maintenant m'y attacher plus sérieusement à la lumiére de la démarche précédente!
merci encore

Caractérisation d'une meilleure approximation

Caractérisation d'une meilleure approximation

Qui est en ligne