Approximation en 1/n
Discussion générale entre passionnés et amateurs de mathématiques sur des sujets mathématiques variés
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 10 Juil 2008, 20:44
par kazeriahm » 10 Juil 2008, 20:44
Salut à tous,
un résultat pas compliqué mais très joli et aux conséquences intéressantes :
montrer que pour tout réel x, il existe une suite
_{n\in \mathbb{N}*})
d'élements de {-1,1} telle que
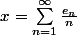
on pourrait ajouter : en déduire que R n'est pas dénombrable
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 10 Juil 2008, 21:24
par Clembou » 10 Juil 2008, 21:24
kazeriahm a écrit:Salut à tous,
un résultat pas compliqué mais très joli et aux conséquences intéressantes :
montrer que pour tout réel x, il existe une suite
_{n\in \mathbb{N}*})
d'élements de {-1,1} telle que
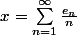
on pourrait ajouter : en déduire que R n'est pas dénombrable
Comment montrer que

ou
)
est en fait la série suivante :
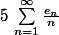
avec
_n \in \{-1,1\})
:briques:
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 10 Juil 2008, 22:16
par skilveg » 10 Juil 2008, 22:16
On peut voir ça comme un cas particulier du théorème de Riemann sur les séries semi-convergentes!
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 10 Juil 2008, 23:16
par aviateurpilot » 10 Juil 2008, 23:16
on peux supposer que
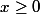
( pour x<0 on travaill avec -x)
soit la suite
)
tel que:
soit
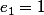
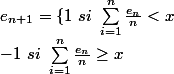
j'ai montrer que dans ce cas
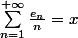
si je n'ai pas fait d'erreur mon raisonnement montre aussi que si
)
une suite tel que
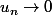
et
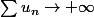
comme le cas de
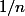
alors il exists
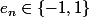
tel que

-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 11 Juil 2008, 01:25
par kazeriahm » 11 Juil 2008, 01:25
oui on est d'accord aviateurpilot c'est tout simple comme résultat en fait mais assez surprenant je trouve
si je note
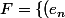_{n \in \mathbb{N*}} \in \{-1;1\}^{\mathbb{N*}} /\sum \frac {e_n}{n} < \infty \})
, est-ce que l'application qui va de F dans R* et qui à
)
associe
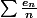
est bijective ?
elle est clairement surjective mais l'injectivité ne me semble pas évidente...
-
Pouick
- Membre Relatif
- Messages: 106
- Enregistré le: 05 Mar 2007, 17:48
-
 par Pouick » 11 Juil 2008, 08:18
par Pouick » 11 Juil 2008, 08:18
le truc, c'est que, comme la série en 1/n diverge, tu peux donc par la méthode dit par aviateurpilot , arreter le processus à un endroit donc genre :
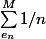
< x
puis aulieu d'ajouter

, juste une fois tu ajoutes -1 .
Puis tu reprends le processus . Au final, tu vas retomber sur x , mais pas avec la même suite... non ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 11 Juil 2008, 09:20
par leon1789 » 11 Juil 2008, 09:20
kazeriahm a écrit:oui on est d'accord aviateurpilot c'est tout simple comme résultat en fait mais assez surprenant je trouve
si je note
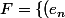_{n \in \mathbb{N*}} \in \{-1;1\}^{\mathbb{N*}} /\sum \frac {e_n}{n} < \infty \})
, est-ce que l'application qui va de F dans R* et qui à
)
associe
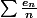
est bijective ?
elle est clairement surjective mais l'injectivité ne me semble pas évidente...
La fonction n'est pas injective.
En posant e_0 = -1, on arrive encore à toucher n'importe quel
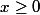
car
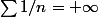

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 11 Juil 2008, 09:21
par leon1789 » 11 Juil 2008, 09:21
Pouick a écrit:le truc (...) Au final, tu vas retomber sur x , mais pas avec la même suite... non ?
on est d'accord :we:
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 11 Juil 2008, 20:10
par aviateurpilot » 11 Juil 2008, 20:10
mon raisonnement montre aussi une generalisation si je n'ai pas fait d'erreur
Si
)
une suite tel que
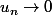
et
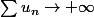
comme le cas particulier de
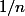
.
et si

bornée tel que
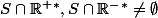
comme le cas particulier de {-1,1}
alors pour tt
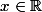
elle existe une INFINITé de suites
\in S^{\mathbb{N}})
tel que

-
miikou
- Membre Rationnel
- Messages: 642
- Enregistré le: 07 Juil 2008, 18:38
-
 par miikou » 12 Juil 2008, 01:12
par miikou » 12 Juil 2008, 01:12
si
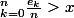
alors
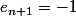
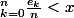
alors
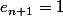
de tel sorte on divise en 2 sous suites Un, lune decroissante minore par x, la seconde croisant majorer par x, la limite vaut x
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
d'élements de {-1,1} telle que
, est-ce que l'application qui va de F dans R* et qui à
associe
est bijective ?