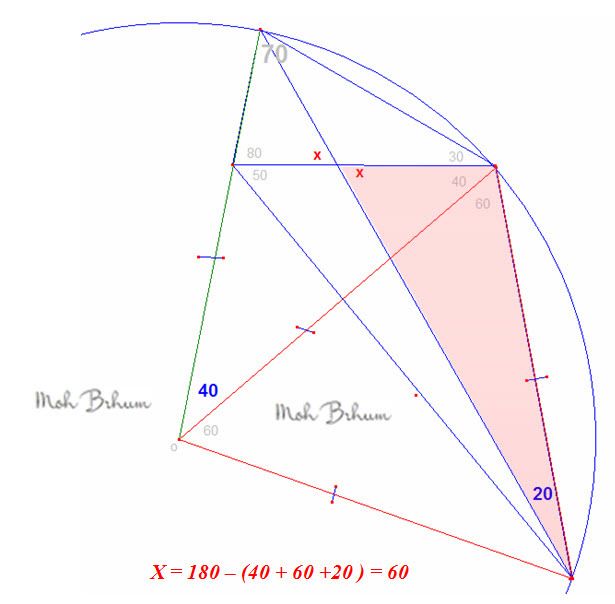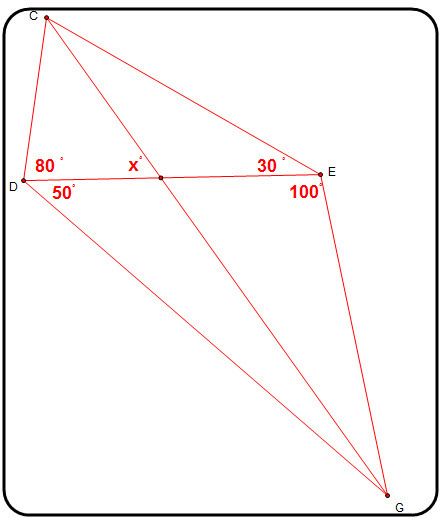
Calculer x

[brhum.moh]

calculer x

[Imod]

Je trouve 60° avec la loi des sinus .

Vu le résultat il y a sûrement une solution moins calculatoire.

Imod

[Ben314]

Salut,
En fait, j'ai l'impression qu'au fond, c'est à peu prés toujours le même dessin "sous jacent" dans ces problèmes.
A savoir celui du polygone régulier à 18 sommets A0,A1,...A17 et de centre O.

Ici, si on prend, G=A0, E=A3, C=A5, D est l'intersection de [A0,A6] et de [A3,A8], alors les diagonales du quadrilatère
(GECD) se coupe en D l'intersection de [A0,A5] et [A3,A8].
Sauf erreur, pour montrer que tout "marche bien", il faut montrer que B est sur [O,A4] (évident par symétrie),
et que D est sur [A0,A6] et sur [OA5] (un peu moins évident)

Mais après, c'est un peu de la "triche" vu qu'on construit un truc qui semble n'avoir aucun rapport pour finalement montrer que c'est le bon dessin (qui est clairement unique à isométrie près).
Donc valable ou pas ???

P.S. : Je me rappelle très bien que c'est toi qui m'avait dit que dans tout ces problèmes là, ce qu'il faut chercher, c'est un cercle.
Ici celui circonscrit à GEC semble "pas mal" et ça se "sent" plus ou moins du fait que 100+30=50+80 donc le symétrique de D par rapport à (GC) est lui aussi sur le cercle...

[Imod]

Oui , d'ailleurs il me semble Mathafou avait fait une étude complète des points de rencontre "fortuits" dans les polygones réguliers : c'est une mine d'exercices aux résultats plutôt bluffants .

Quand on a compris le truc , ça devient vite lassant même si je me laisse encore avoir régulièrement :marteau:

Imod

[Ben314]

Moi aussi, ça continue régulièrement à m'amuser.
Par exemple là, je sais pas trop comment faire pour rendre la démarche "directe", i.e. tout construire en partant de la figure donnée et faire uniquement des "déduction".

L'autre truc marrant (je pense que tu me connait suffisamment pour t'en douter...) c'est aussi de trouver une solurion dans laquelle le fameux cercle ne "se voit pas trop"... :zen:

[brhum.moh]

Bonjour à tous


Voici la solution




Je essayé Y at-il une seconde solution