A l'attention d'Oktave

[Jota Be]

On commence par un exo tout frais créé :

1) Montrer que -1 est une racine de
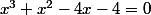
2) Trouver une factorisation de
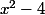
3) Déduire des deux questions précédentes toutes les solutions de

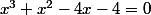
[Jota Be]

Les solutions sont -1; +2; -2.
Merci :happy3: un autre ?

Haha bravo :ptdr:
A ce rythme là, la demande va être bien trop importante par rapport à la production !

[Lostounet]

Haha bravo :ptdr:
A ce rythme là, la demande va être bien trop importante par rapport à la production !

Résoudre


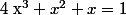
:we:

[Jota Be]

Allez un autre, comme tu te débrouilles :

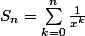
On admet que la suite des sommes partielles donnée par converge absolument.
Calculer :

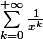
[Euler07]

Résoudre


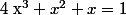
:we:

Tu avais pas plus simple ?

:livre:

[Jota Be]

Vi on avait dit facile les gars !
Pour la suite va falloir que j'aille chercher des vieux cours et que je relise le tout car à part l'histoire grec de la flèche qui fait la moitié du trajet, puis le quart, puis le huitième et ainsi de suite jusqu'à arriver (pour expliquer que 1/2 + 1/4 + 1/8 + 1/16 + ...etc =1 ) je ne me souviens plus des formule pour les suites !
Mais bon le raisonnement fait par les grec avec la moitié, puis la moitié de la moitié, puis la moitié de la moitié de la moitié etc doit être valable avec le tiers ? Puis le tiers du tiers, puis le tiers du tiers du tiers etc ... ça ferait 1 à la fin aussi !?
Et intuitivement je me dit que tant que x supérieur à 1 ça doit marcher ? Ça doit converger à 1 !?
Mais pour le prouver faudrait que je retourne voir les cours.

Pour l'équation de Lostounet dsl, 3° degrés je n'ai jamais appris à les faire de toute ma vie.
Je ne vois pas de solution évidente non-plus. C'est pô zéro c'est pô un ...
Intuitivement je pense que x doit pô être superieur à 1 ... je peux pô en dire plus ...

Vous allez trop loin là les gars !
Beaucoup trop loin. Faut que je me remette dans le bain en commençant par du trés facile, pô du trop dur !

Je te garantis que mon truc est bien plus facile que celui de Lostounet :zen: Dès lors que tu connais l'expression adéquate dans ce cas-là (voir discussion avec Chaa).
Je sèche sur l'équation
Aussi, je suis allé sur WA et l'unique solution réelle n'est pas facile du tout à trouver. Bref, faut du boulot !

[Lostounet]

Aussi, je suis allé sur WA et l'unique solution réelle n'est pas facile du tout à trouver. Bref, faut du boulot !

Je l'ai résolue hier (avec les formules devant moi). C'est vraiment pas si dur (enfin, j'ai bêtement appliqué les formules mais c'est mieux que rien!).

Je peux poster si vous voulez.

[Jota Be]

Je l'ai résolue hier (avec les formules devant moi). C'est vraiment pas si dur (enfin, j'ai bêtement appliqué les formules mais c'est mieux que rien!).

Je peux poster si vous voulez.

Haha merci mais on va chercher encore un peu
Ou tu peux spoiler discrètement sinon ! Lorsqu'on sèchera vraiment trop on regardera

[Lostounet]

Mais sinon y'a pas vraiment d'astuce à part Tschirnhaus.

[Lostounet]

Si par formule tu entends "discriminant qui permet de résoudre les équations du 3° degrés" ça sera sans moi !
J'ai longtemps essayer de résoudre (sans succés) des équations du second dégrés avant que je ne connaisse le discriminant pour le 2° degrés, et bah je m'y ré-amuserait pô !
Si il n'ya pas d'astuce particulière pour celle ci. Si c'est par le discriminant pour le 3° degrés qui résoud ton équation et rien d'autre il est inutile de s'y acharner. On ne va pas réinventer le discriminant du 3° degrés.

Bah justement je ne me souviens plus des formules.

Inutile de s'y acharner?
Pour toi, peut-être. Mais j'aime bien le faire, moi :we:
T'es pas obligé lol

[Jota Be]

Si par formule tu entends "discriminant qui permet de résoudre les équations du 3° degrés" ça sera sans moi !
J'ai longtemps essayer de résoudre (sans succés) des équations du second dégrés avant que je ne connaisse le discriminant pour le 2° degrés, et bah je m'y ré-amuserait pô !
Si il n'ya pas d'astuce particulière pour celle ci. Si c'est par le discriminant pour le 3° degrés qui résoud ton équation et rien d'autre il est inutile de s'y acharner. On ne va pas réinventer le discriminant du 3° degrés.

Il n'existe pas de technique de discriminant pour des équations polynomiales d'ordre >2 d'après ce que j'en sais. Inutile donc d'aller voir de ce côté-là.

[Lostounet]

Moi ce que je dis c'est que j'avais prévus de réviser tranquillement en fesant plein de petit exos facile.

C'est pas ça qui manque. N'importe quel livre parascolaire. Et y'a plein de sites très bien fait pour ce genre d'exercices.

[Jota Be]

Faut quand même dire que Tschirnhaus ça décourage vite :ptdr:
J'ai essayé tout seul de faire un exemple au hasard et ça me prend déjà à griser une page et demie...
Il n'y en a pas d'autre pour résolution générale de polynômes ?

[Jota Be]

Je l'ai résolue hier (avec les formules devant moi). C'est vraiment pas si dur (enfin, j'ai bêtement appliqué les formules mais c'est mieux que rien!).

Je peux poster si vous voulez.

Finalement, je veux bien que tu postes ! Si ça ne te dérange pas bien sûr

[Zweig]

Résoudre


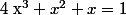
:we:

T'es sûr ? Ok y a une racine (réelle) mais elle est loin d'être triviale ...