Aidez moi : inverse modulo n - démonstration-rectif

[prof007]

Bonjours a tous :
pouvez vous m'aider a démontrer l'existence et l'unicité de l'inverse modulo n mais sans utiliser ni Bézout ni l'ordre
:)
Merci beaucoup

[adrien69]

Salut,





Plus sérieusement avec la loi multiplicative, c'est faux si n n'est pas un nombre premier...
Mais admettons que c'en soit un. Alors soit k dans [1,n-1] comme on peut démontrer le petit théorème de Fermat sans les deux interdits je me permets de l'utiliser.

On a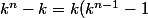 qui est divisible par n or k et n premiers entre eux, on a alors le théorème de Gauss (ou lemme d'Euclide, encore moins fort), donc est divisible par n et on a l'existence. L'unicité vient du fait que Z/nZ est un anneau pour la loi multiplicative, donc si inverse il y a, il est unique.

[adrien69]

(Bien sûr ce n'est valable que si n est strictement supérieur à 2, mais j'espère que tu n'as pas besoin de moi pour traiter ce cas)

[leon1789]

Bonjours a tous :
pouvez vous m'aider a démontrer l'existence et l'unicité de l'inverse modulo n mais sans utiliser ni Bézout ni l'ordre

Merci beaucoup

Question étrange car :

-1- l'existence n'est pas assurée à tous les coups : la définition dit que, pour que un entier a soit inversible modulo n, il faut que a et n vérifie une relation de Bézout, donc pgcd(a,n)=1.
Il existe bien des manières pour démontrer qu'en élément est inversible (lorsqu'il l'est...) mais tout cela dépend des circonstances : il n'y a pas de preuve "prête à l'emploi".

-2- l'unicité ne requiert pas du tout Bézout ni l'ordre ! Soit b et c deux inverses de l'entier a modulo n :
modulo n, on a ab=1 et ac=1, donc b = b(ac) = (ba)c = c

[leon1789]

Bonjours a tous :
pouvez vous m'aider a démontrer l'existence et l'unicité de l'inverse modulo n mais sans utiliser ni Bézout ni l'ordre

Merci beaucoup

Question étrange car :

-1- l'existence n'est pas assurée à tous les coups : la définition dit que, pour que un entier a soit inversible modulo n, il faut que a et n vérifie une relation de Bézout, donc pgcd(a,n)=1.
Il existe bien des manières pour démontrer qu'en élément est inversible (lorsqu'il l'est...) mais tout cela dépend des circonstances : il n'y a pas de preuve "prête à l'emploi".

-2- l'unicité ne requiert pas du tout Bézout ni l'ordre ! Soit b et c deux inverses de l'entier a modulo n :
modulo n, on a ba=1 et ac=1, donc b = b(ac) = (ba)c = c (on utilise l'associativité de la multiplication).

[prof007]

avant tout merci beaucoup :)
je vois que ma question est un peut tirée par les cheveux désolé je suis pas habitué donc je reprend ma question :
Soit a et b deux entiers naturels non nuls tel que : b>=2 et PGCD(a,b)=1 ( premiers entre eux ). Montrer qu'il existe un seul entier k dans {0,1,2,..., n - 1} tel que a.k =1 ( mod b ) .
voila .

[prof007]

j'ai trouvé ceci " ca me plait pas trop ":
soit i dans {0,1,..,n-1} .
je montre que pour tout i il existe un unique Ri de {0,1,..,n-1} tel que a*i=Ri (mod n) ( une bijection ) (.. ) cela fait le cas particulier Ri=1 répond a la question .
(..)
soit 0<=ia*i = aj mod(n) eq a : i = j mod(n) ( car a et n premiers entre eux ) éq a : n divise (i - j ) ce qui est absurde ( i - j < n )

un avis s'il vous plait ou meilleur démonstration
merci beaucoup