Cercle médiateur
Olympiades mathématiques, énigmes et défis
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 03 Juil 2009, 19:45
par Imod » 03 Juil 2009, 19:45
Bonsoir :chef:
On considère
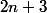
points tels que trois d'entre eux ne sont jamais alignés et quatre jamais cocycliques . Existe-t-il un cercle passant par trois de ces points avec

points à l'intérieur et

à l'extérieur ?
Amusez-vous bien :zen:
Imod

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 03 Juil 2009, 20:14
par nuage » 03 Juil 2009, 20:14
Salut,
pour

c'est évidement possible.
Pour
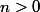
je m'interroge sur le sens de
Imod a écrit:avec n points à l'intérieur et n à l'extérieur
Est-ce au moins

?
ou le nombre de points serait-il
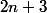
?
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 03 Juil 2009, 20:19
par Imod » 03 Juil 2009, 20:19
nuage a écrit:ou le nombre de points serait-il
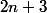
?
C'est ça :marteau: :marteau:
Imod

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 03 Juil 2009, 20:26
par nuage » 03 Juil 2009, 20:26
je dirais que le principe de tiroirs permet de conclure.
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 05 Juil 2009, 16:46
par Imod » 05 Juil 2009, 16:46
nuage a écrit:je dirais que le principe de tiroirs permet de conclure.
Pourquoi pas mais il faudrait préciser qui sont les tiroirs et les chaussettes :zen:
Imod
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 08 Juil 2009, 18:22
par Imod » 08 Juil 2009, 18:22
Un petit "UP" pour ce problème , certes facile , mais un peu vite expédié quand même :zen:
Imod
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 10 Juil 2009, 04:37
par nodjim » 10 Juil 2009, 04:37
Je n'ai rien compris à l'échange avec nuage.
Sinon, soit le nuage de points. Il existe un grand cercle qui passe par les 3 points extérieurs et dont tous les autres points sont à l'intérieur. On peut construire un cercle plus petit tel que l'on trouvera un point et un seul à l'extérieur. Etc...
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 10 Juil 2009, 10:00
par Imod » 10 Juil 2009, 10:00
Si tu veux nodjim .
D'une façon un peu plus rigoureuse , si
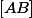
est un côté de l'enveloppe convexe des
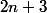
points et que l'on note

,

, ... ,

les autres points , comme tous ces points sont du même côté de [AB] , par la propriété de l'angle inscrit , les angles

sont tous distincts . Par exemple

et alors le cercle passant par

,

et
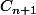
laisse les points

, ... ,

à l'extérieur et

, ...

à l'intérieur .
Imod
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 10 Juil 2009, 10:36
par lapras » 10 Juil 2009, 10:36
Moi j'attend toujours les tiroirs de nuage ;)
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 12 Juil 2009, 07:47
par nodjim » 12 Juil 2009, 07:47
Imod a écrit:Si tu veux nodjim .
D'une façon un peu plus rigoureuse , si
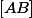
est un côté de l'enveloppe convexe des
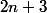
points et que l'on note

,

, ... ,

les autres points , comme tous ces points sont du même côté de [AB] , par la propriété de l'angle inscrit , les angles

sont tous distincts . Par exemple

et alors le cercle passant par

,

et
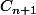
laisse les points

, ... ,

à l'extérieur et

, ...

à l'intérieur .
Imod
D'accord, c'est mieux
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités
est un côté de l'enveloppe convexe des
points et que l'on note
,
, ... ,
les autres points , comme tous ces points sont du même côté de [AB] , par la propriété de l'angle inscrit , les angles
sont tous distincts . Par exemple
et alors le cercle passant par
,
et
laisse les points
, ... ,
à l'extérieur et
, ...
à l'intérieur .