La conjecture de Fermat fausse

bonjour,

on définit par les nombres de fermat.

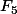
démontrer sans calcul que est divisible par 641.

avant j'ai démontrer que si était premier alors a est pair et n une puissance de 2.

ca fait pas mal de temps que je suis dessus et ca ma pas l'air évident...

Salut J-R !
On remarque que
641 = 2^7 * 5 + 1
donc
2^7*5 = -1 [641]
"Remarque" que 5^4 = -16 = -2^4 [641]
donc
(2^7*5)^4 = 2^(28) * - 2^4 = 1 [641]
donc
2^32 = - 1 [641]
cqfd

F5 = 2^32 + 1
Supposons que F5 admette un diviseur premier p
p = 2^6k + 1 = 64k + 1

Pour k = 10, p = 641
2^16 = 65536 =641 x 102 + 154 donc congrue à 154 modulo 641
2^32 congrue à 154^2 = 23716 = 641x36 + 640 congrue à -1 modulo 64&
Donc 2^32 + 1 congrue à 0 modulo 641

:doh:

merci à vous deux :zen: