Pb de notations bis

Pour les notations des dérivées "à la physicienne" on utilise svt dA(t)/dt ou delata minuscule à la place de d.
Quelle difference.Qd utiliser l'une? l'autre

Il me semble que les physiciens notent 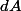une différentielle exacte, c'est-à-dire la vraie différentielle d'une fonction, et qu'ils notent une forme différentielle qui n'est pas exacte. Intuitivement, il s'agit toujours d'un accroissement infinitésimal de la quantité , mais seul le premier cas correspond à la différentielle d'une fonction au sens mathématique.
Cette distinction est particulièrement importante en thermodynamique si ma mémoire est bonne (y a-t-il un physicien dans l'assistance ? j'ai peur de dire des bêtises).

Par exemple, considérons le travail élémentaire d'une force dans l'espace muni d'un repère avec les coordonnées :
.
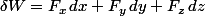C'est une forme différentielle. Il n'y a a priori aucune raison pour que ce travail dérive d'un potentiel, c'est-à-dire pour qu'il existe une fonction des trois variables de l'espace telle que :
,
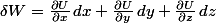c'est-à-dire pour que les , et soient les dérivées partielles d'une même fonction .
Lorsque c'est le cas, on a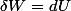 , où est la différentielle exacte de la fonction , vérifiant :
.
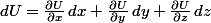C'est la différentielle d'une fonction de trois variables, au vrai sens mathématique du terme.

Je n'ai pas compris pourquoi tu as recrée un topic ? Nos réponses ne te suffisaient pas ? Dans ce cas là il suffisait de nous le dire dans l'autre topic, pas besoin d'en créer un autre...

:triste:
Jord

Cher Nightmare, il s'agit d'une question distincte de la précédente, à partir de quoi, ouvrir un nouveau fil me semble justifié.

Pas vraiment, il est certes question de delta au lieu de d ronde mais on parle toujours de notation pour les dérivées et les différences avec les physiciens, il aurait pu trés bien ajouter à la suite de l'autre topic : " et quand est-il alors de la différence entre Delta et d". Enfin je ne suis pas modérateur ici ce n'est pas à moi d'en décider.


Jord

D'après le précédent message de Nightmare, il semblerait qu'on ait besoin de l'intervention d'un modérateur :happy3: . Ca tombe bien, je suis là!

Je pense que les questions étaient certes distinctes, mais en grand rapport l'une avec l'autre. Je crois donc qu'il aurait mieux valu adopter la solution proposée par Nightmare, mais il n'y a aucune gravité dans le fait d'utiliser deux discussions au lieu d'une, et puis, maintenant, c'est fait.

J'aurais bien aimé discuter de ce sujet avec d'autres modérateurs avant de donner mon avis, mais en ce moment, ils se font plutôt rares...

Donc selon moi, il n'y a aucun problème, mais à l'avenir, pensez que si la question suivante a un très grand rapport avec la 1ère, mieux vaut la poser dans la même discussion.

:happy3:

Désolé si je risque de faire dériver le fil, mais la première intervention de Nightmare montre clairement qu'il n'avait pas saisi la différence entre les deux questions, puisqu'il pensait que l'intervenant reposait la même question car les premières réponses n'auraient pas été satisfaisantes ; or il ne s'agit pas du tout de la même question !
Si j'ai trois questions distinctes sur un même sujet, mais indépendantes, dois-je les poser dans le même fil, au risque d'en rendre la lecture difficile, avec les réponses qui s'entremêleront ? Personnellement, je préfère trois fils différents, d'autant plus que certains contributeurs peuvent ne pas être intéressés par toutes les questions.

Oui en effet phenomen a lors de la rédaction de mon premier message je pensais que c'était les mêmes questions mais suite à votre réaction j'ai crée un second message toujours en restant sur mes positions mais cette fois ci en sachant que les message étaient différent (je vous ai d'ailleur fait part de la différence). Quoi qu'il en soit le Modérateur a tranché, la discussion est alors close.
En effet il est possible qu'au fil des conversations sur des sujets peu différent dans un même topic, celui-ci devienne illisible, mais il en adviendrait de même du forum si tout le monde créait 50 topics par questions alors qu'elles sont relatives à un même sujet.
Ici ce n'est pas bien grave comme le dit alpha, il n'y a que deux topics, mais il n'est pas rare de voir des personnes ayant tout un tas de question à poser mais prefere les poser une par une. Dans ce cas là il est bien préférable qu'il le fasse dans un même topic.

Enfin encore une fois ce n'est pas moi qui gére ce forum, j'ai posté mon premier message en guise de remarque et non d'obligation. Si malgrés tout le posteur décide de continuer à poster à sa façon, c'est aux modérateurs d'agir et non à moi.


Jord

*** Edit Moi-même : Il est préférable de clore ce sujet maintenant car nous sommes en train de débattre sur l'illisibilité de certains posts or la conversation que nous tenons en ce moment ne facilite pas la lisibilité de ce post***

Il est vrai que la lecture est d'autant moins facile que la discussion est longue, et d'autant plus facile que toutes les discussions distinctes sont clairement séparées.

Tout bien réfléchi, je crois que vous pouvez, si c'est VRAIMENT justifié, créer 2 discussions, mais il ne faudrait pas que certains prennent l'habitude de créer plusieurs discussions sur le même sujet ou sur un même type d'exos quand ce n'est pas nécessaire, comme c'est malheureusement parfois le cas (exemple : j'ai une question sur les coordonnées cylindriques... puis une autre(toujours sur les coordonnées cylindriques = 2 discussions :hum: ) ).

Sans compter que poster trop de discussions nuit aussi à la lisibilité du forum.

:happy3: