Notations O

[saifert]

Bonjour,
voici un pbme :

Soient et deux fonctions reelles en un point de R. On dit que est un grand de au voisinage de apartenant aux reels si il existe une fonction reelle bornee telle que pour tout x dans un voisinage de on a On note

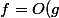1)Montrer que si et sont deux grands de alors + aussi, ainsi que pour tout apartenant aux reels.

j'ai commence par :
=
mais je n'arrive pas a continuer.
:help:
merci de votre aide.

[serge75]

Ecris ta définition pour f1 et f2 ; puis la somme de deux fonctions bornées en est une...
PS : pour le coup ton pseudo est malheureux ! lol

[saifert]

ui.... :marteau: ... si evident que ca ?

oui, ben je sais qu'il est assez drole mon pseudo vu les circonstances, mais il ne faut pas le lire en francais. :happy2:

[serge75]

Désolé pour l'humour sur ton pseudo mais il faut avouer ici que c'était tentant !
Bon reprenons :
De f1=O(g) tu tires f1=h1.g avec h1 bornée. De même f2=h2.g.
Alors f1+g1=(h1+h2).g avec h1+h2 bornée comme somme de fonctions bornées.
Tu fais la même pour af avec a réel ou complexe.

[saifert]

ok... merci
en fait j'avais pense a ca, mais il semblait si "elementaire" que j'ai pense, que c'etait faux.

[serge75]

voilà, maintenant tu sais faire..... OK je sors !