Petites Questions
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Anonyme
 par Anonyme » 22 Sep 2007, 12:47
par Anonyme » 22 Sep 2007, 12:47
Bonjour, comment justifie t-on que
quelque soit x>0, 1-(1/x)< (Ex/x) < ou = à 1
et en deduire lim->+oo de (Ex)/x
Merci!
-
gol_di_grosso
- Membre Irrationnel
- Messages: 1402
- Enregistré le: 22 Sep 2007, 11:28
-
 par gol_di_grosso » 22 Sep 2007, 12:56
par gol_di_grosso » 22 Sep 2007, 12:56
Ex ?=? exp(x)
et si c ca exp(x)/x >>>>1 pour x très grand
-
Anonyme
 par Anonyme » 22 Sep 2007, 13:00
par Anonyme » 22 Sep 2007, 13:00
Dans le coursc'est defini comme ca: Soit x un reel E(x), la partie entiere de x, est la plus grand entier relatif inférieur ou égal à x.
-
gol_di_grosso
- Membre Irrationnel
- Messages: 1402
- Enregistré le: 22 Sep 2007, 11:28
-
 par gol_di_grosso » 22 Sep 2007, 13:11
par gol_di_grosso » 22 Sep 2007, 13:11
a ok dsl
x>0
donc t'a
 \le x)
(par définition)
et ainsi
} {x} \le 1)
ensuite
+1)
car E(x) plus petit entier inférieur ou égal à x enfin tu vois (non ?)
)
}{x}<\frac{E(x)}{x})
et
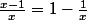
-
Anonyme
 par Anonyme » 22 Sep 2007, 14:51
par Anonyme » 22 Sep 2007, 14:51
Ui je vois et la limite est 0 ? nan ?
-
gol_di_grosso
- Membre Irrationnel
- Messages: 1402
- Enregistré le: 22 Sep 2007, 11:28
-
 par gol_di_grosso » 22 Sep 2007, 17:44
par gol_di_grosso » 22 Sep 2007, 17:44
nan enfaite c'est 1
théorème des gendarme (non?)
en l'infini
-1/X tend vers 0
1-1/x tend vers 1
et t'a fonction est encadrée par 1-1/xdonc enfaite ça tendrais plutôt vers 1
exemple
10000/10000.3333=0.999996...
10000/10000=1
10000/10000.999999=0.999900010099
-
Anonyme
 par Anonyme » 22 Sep 2007, 20:40
par Anonyme » 22 Sep 2007, 20:40
Ah ui c'est le theoreme des gendarmes =)
Merci de m'avoir expliqué, j'ai compris xD :we:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
