[MP] Un résultat sur les suites
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
euler21
- Membre Relatif
- Messages: 313
- Enregistré le: 26 Aoû 2009, 02:40
-
 par euler21 » 30 Oct 2010, 12:22
par euler21 » 30 Oct 2010, 12:22
Bonjour
On se propose dans un exercice de démonter que si

est une suite à valeurs positives décroissante et telle que la série de terme général

converge, alors
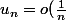)
. J'ai rédigé une solution et je ne sais pas si c'est correct.
Comme la série converge, elle est de Cauchy et de plus la suite

tend vers 0.
Soit
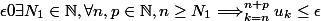
( Les valeurs absolues n'étant pas nécessaires puisque la suite

est positive.
Et puis
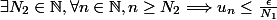
(c'est ce choix de
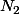
dont je ne suis pas sûr puisqu'il implique
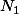
)
Soit
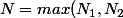+1)
soit
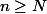
alors

D'où le résultat demandé. Est ce que c'est correct ??
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 30 Oct 2010, 12:34
par girdav » 30 Oct 2010, 12:34
Bonjour,
dans la dernière ligne juste avant le dernier signe

comment majores-tu la somme?
Sinon, je crois qu'il y a une preuve qui ne fait pas appel (explicitement) aux

: on a
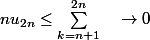
quand
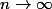
et on peut montrer aussi que la suite de terme général
u_{2n+1})
converge vers

.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 30 Oct 2010, 12:35
par Nightmare » 30 Oct 2010, 12:35
Salut,
dans ta dernière ligne, pourquoi
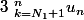
s'est transformé en
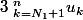
?
-
euler21
- Membre Relatif
- Messages: 313
- Enregistré le: 26 Aoû 2009, 02:40
-
 par euler21 » 30 Oct 2010, 12:39
par euler21 » 30 Oct 2010, 12:39
Bonjour
Pour la majoration, on a
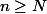
donc je peux appliquer la majoration sur le premier terme, à savoir
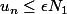
et puis pour le deuxième terme on utilise le fait que la série vérifie le critère de Cauchy, et j'ai remplacé le terme

par
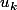
parce que la suite est décroissante.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 30 Oct 2010, 12:55
par Ben314 » 30 Oct 2010, 12:55
Salut,
Ca m'a l'air tout à fait correct.
Perso, j'aurais dit que, si on pose
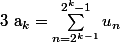
alors

est convergente donc
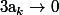
.
De plus,
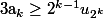
(nombre de termes multiplié par un minorant des termes).
Pour tout
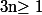
, si
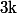
est tel que

(donc
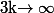
lorsque
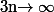
) on a
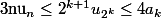
ce qui prouve que
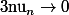
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
euler21
- Membre Relatif
- Messages: 313
- Enregistré le: 26 Aoû 2009, 02:40
-
 par euler21 » 30 Oct 2010, 13:02
par euler21 » 30 Oct 2010, 13:02
Salut Ben
Dans ta démonstration, ça ressemble un peu au critère de condensation de Cauchy. Je la trouve très subtile :++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités