Intégrale d'une racine

[upium666]

Bonjour à tous et à toutes !

Que vaut ?
Et plus particulièrement ? (pour )

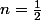
Pourquoi n'existe-t-il pas de solution générale à ce que j'ai vu ?
Je veux dire : Sur quoi bloquent les mathématiciens pour ce problème ?

Merci

(Remarque : Quelle serait l'utilité de la piste suivante ?


alors


)

[tototo]

[quote="upium666"]Bonjour à tous et à toutes !

Que vaut ?
si on avait = f^(n+1)(b)-f^(n+1)(
Et plus particulièrement ? (pour )

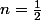
Pourquoi n'existe-t-il pas de solution générale à ce que j'ai vu ?
Je veux dire : Sur quoi bloquent les mathématiciens pour ce problème ?

Merci

(Remarque : Quelle serait l'utilité de la piste suivante ?


alors


)

[alexandre ouimet]

Salut, peut-être que je ne comprend juste pas ton problème, mais en ne posant qu'un simple changement de variable ne serais-tu pas capable d'avoir une constante fois l'intégrale de u^(1/2)??
Cela te donnerais alors k((2/3)*u^(3/2)) je pense...
en tout cas laisse moi savoir j'ai toute ma vie devant moi :lol3: