Bonjour a tous, j'ai un exercice de maths mais je ne comprend pas vraiment l'exercice suivant :
Image de l'exercice (désolé l'image est a 90°)
Exercice de math dm de 3eme
4 messages
- Page 1 sur 1
a) On sais que ABCD est un rectangle.
Ainsi :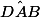 ,
, 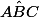 ,
, 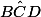 et
et 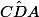 sont des angles droits (90°).
sont des angles droits (90°).
De ce fait :
- QAM est un triangle rectangle en A (car Q [AD] et M
[AD] et M [AB])
[AB])
- MBN est un triangle rectangle en N (car M [AD] et N
[AD] et N [BC])
[BC])
- NCP est un triangle rectangle en C (car N [BC] et P
[BC] et P [CD])
[CD])
- PDQ est un triangle rectangle en D (car P [CD] et Q
[CD] et Q [AD])
[AD])
Or : l'aire d'un triangle rectangle est calculée à partir du produit des côtés formant l'angle droit, le tout divisé par deux.
De façon moins verbale, un triangle rectangle ABC, rectangle en A, a pour aire :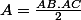 .
.
Ainsi nous avons :
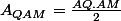
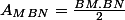
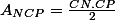
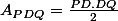
Or : AQ = AD-QD = BC-QD = 1 cm.
BM = AB-AM = 3 cm.
CN = AQ = 1 cm, car AD = BC et QD = BN.
DP = BM, car AB = DC et AM = PC.
Ainsi on obtient au final :
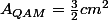
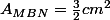
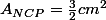
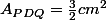
De ce fait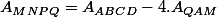 , étant donnée que l'aire des triangles sont identiques.
, étant donnée que l'aire des triangles sont identiques.
Or :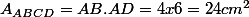 .
.
On obtient alors :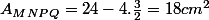
b) A la question précédente, nous avons établit :
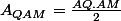
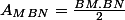
Or AQ = AD-x = 4-x
AM = x
MB = AB-x = 6-x
BN = x
Ainsi on obtient :
.x}{2})
.x}{2})
c) On pose f(x) l'aire du quatrilatère MNPQ.
=A_{ABCD}-2.(A_{QAM}+A_{MBN})) , car QAM et NPC sont isométriques, ainsi que MBN et PDQ. [isométrique = de même mesure].
, car QAM et NPC sont isométriques, ainsi que MBN et PDQ. [isométrique = de même mesure].
Nous avons établis que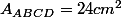 et que
et que .x}{2}) ,
, .x}{2}) .
.
Donc :=24-2.(\frac{(4-x).x}{2}+\frac{(6-x).x}{2}))
On développe=24-2.(\frac{4x-x^2}{2}+\frac{6x-x^2}{2}))
On réduis=24-2.(5x-x^2))
On développe, attention au signe MOINS = 24-10x+2x^2)
On organise=2x^2-10x+24) .
.
d) (1) Non, en classe de 3ème je ne sais pas encore résoudre des équations du second degré (avec des x²).
(2) Bon après remplir le tableau tu remplaces x par les valeurs de la ligne du haut dans l'expression de f(x).
(3) Représenter graphiquement c'est placé l'ensemble des points de coordonnée (x,f(x)), donc ligne du haut du tableau en abscisse, ligne du bas en ordonnée.
(4) Sur ton graphique tu traces une droite parallèle à l'axe des abscisses passant par 13.5 en ordonnée.
Et tu regardes les abscisses des points de l'intersection de la courbe de ta fonction avec la droite tracée, c'est les solutions.
(5) L'aire minimale, c'est la plus petite valeur positive que prend f, donc l'abscisse du point le plus bas dans la partie supérieure du graphique.
Ainsi :
De ce fait :
- QAM est un triangle rectangle en A (car Q
- MBN est un triangle rectangle en N (car M
- NCP est un triangle rectangle en C (car N
- PDQ est un triangle rectangle en D (car P
Or : l'aire d'un triangle rectangle est calculée à partir du produit des côtés formant l'angle droit, le tout divisé par deux.
De façon moins verbale, un triangle rectangle ABC, rectangle en A, a pour aire :
Ainsi nous avons :
Or : AQ = AD-QD = BC-QD = 1 cm.
BM = AB-AM = 3 cm.
CN = AQ = 1 cm, car AD = BC et QD = BN.
DP = BM, car AB = DC et AM = PC.
Ainsi on obtient au final :
De ce fait
Or :
On obtient alors :
b) A la question précédente, nous avons établit :
Or AQ = AD-x = 4-x
AM = x
MB = AB-x = 6-x
BN = x
Ainsi on obtient :
c) On pose f(x) l'aire du quatrilatère MNPQ.
Nous avons établis que
Donc :
On développe
On réduis
On développe, attention au signe MOINS
On organise
d) (1) Non, en classe de 3ème je ne sais pas encore résoudre des équations du second degré (avec des x²).
(2) Bon après remplir le tableau tu remplaces x par les valeurs de la ligne du haut dans l'expression de f(x).
(3) Représenter graphiquement c'est placé l'ensemble des points de coordonnée (x,f(x)), donc ligne du haut du tableau en abscisse, ligne du bas en ordonnée.
(4) Sur ton graphique tu traces une droite parallèle à l'axe des abscisses passant par 13.5 en ordonnée.
Et tu regardes les abscisses des points de l'intersection de la courbe de ta fonction avec la droite tracée, c'est les solutions.
(5) L'aire minimale, c'est la plus petite valeur positive que prend f, donc l'abscisse du point le plus bas dans la partie supérieure du graphique.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
