Au dîner du roi..

[benekire2]

Bonjour, voici une énigme que l'on m'a proposée hier.

On offre 1000 bouteilles de vin au Roi et ce dernier a eu l'information qu'une bouteille est empoisonnée et que le poison agit en une heure exactement. Le dîner commence dans exactement une heure. Combien lui faut-il de servants pour goûter les vins et déceler la bouteille empoisonnée ? (on recherche le nombre minimal)

Pour ceux qui connaissent le problème recommencer en supposant que 2 bouteilles sont contaminées (pour ce problème là je n'ai pas la réponse encore ...)

Pour ceux qui sont très fort, le cas où $n$ bouteilles sont contaminées, nombre minimal de goûteurs ? Ou asymptotique du nombre de goûteurs ?

Bonne et heureuse année 2016 !

[Matt_01]

Je dirais que c'est de l'ordre de

[benekire2]

Oui c'est aussi mon asymptotique mais sans preuve bien évidemment. Pour le nombre minimal pour n=2 je n'ai pas réussi à descendre sous 60

[Matt_01]

Il me semble que c'est faisable avec 19.
Des que j'ai le temps j'explique comment.

[Matt_01]

En fait je suis pas certain de pouvoir faire en 19.
Mais vu qu'on peut faire avec 10 pour n=1, on peut facilement faire 20 avec n=2.
J'ai pas vraiment le temps d'y reflechir maintenant, mais je m'y mets quand j'ai le temps.

[Ben314]

Mais vu qu'on peut faire avec 10 pour n=1, on peut facilement faire 20 avec n=2.

Perso, ça me semble pas très clair le coup du 2x10=20. Tu peut expliciter comment tu ferais partant de la méthode avec 10 testeurs pour une bouteille empoisonnée pour en déduire une méthode avec 20 testeurs pour deux bouteilles empoisonnées ?
Perso, pour le moment, tout ce que j'arrive a dire, c'est que si on veut y arriver avec un minimum de testeurs, il faut que chacun d'eux teste environ 293 bouteilles (pour n assez grand, il faut que chaque testeur goûte bouteilles)

[nodjim]

S'il y a 10 goûteurs, on les modélise par un rang d'une puissance de 2. Comme 2^10=1024, il suffit de donner à chaque bouteille un nombre binaire compris entre 1 et 1000. Par exemple la bouteille 37 vaut en binaire: 100101. Ce sont les goûteurs 1 4 et 6 qui testeront cette bouteille. Si ce sont les goûteurs 1, 4 et 6 qui sont malades, alors on saura que c'est la bouteille 37 qui était empoisonnée.

[Matt_01]

Perso, ça me semble pas très clair le coup du 2x10=20. Tu peut expliciter comment tu ferais partant de la méthode avec 10 testeurs pour une bouteille empoisonnée pour en déduire une méthode avec 20 testeurs pour deux bouteilles empoisonnées ?
Perso, pour le moment, tout ce que j'arrive a dire, c'est que si on veut y arriver avec un minimum de testeurs, il faut que chacun d'eux teste environ 293 bouteilles (pour n assez grand, il faut que chaque testeur goûte bouteilles)

Ok autant pour moi j'avais pas lu l'histoire du "une heure exactement" ie chaque testeur boit au même moment.

[Robot]

Sans limite de temps, 11 goûteurs suffisent pour savoir à coup sûr quelles sont les deux bouteilles empoisonnées (sachant qu'un goûteur non empoisonné peut regoûter). On peut peut-être faire mieux.

[nodjim]

C'est une question ouverte, en fait, où il s'agira plus de performance au cas par cas que réellement une formule qui marche à tous les coups. Le 60 de benekire pour n=2 n'est pas mal du tout.

[benekire2]

Je pense qu'on peut faire bien moins ...

[nodjim]

L'idéal est la formule de Matt, soit 20 environ pour n=2.

[Robot]

Il est facile de voir que 19 est une borne inférieure pour le nombre cherché.

[Ben314]

Comme a priori, je vois pas trop le cas général, je commencerais bien par essayer une valeur plus petite.
Par exemple, avec 5 "testeurs" il y a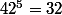 issues possibles et le plus grand [TEX]4$\ {n\choose 2} Peut on trouver 2 bouteilles empoisonnées parmi 8 avec 5 "testeurs" ?

EDIT : sauf erreur, la réponse est NON.

[nodjim]

Sauf erreur, cette combi: 0 4 8 14 16 28 1 31 ne donne que des sommes différentes.

[nodjim]

Je l'ai bien caché mon 32.

[Ben314]

Sauf erreur, cette combi: 0 4 8 14 16 28 1 31 ne donne que des sommes différentes.

C'est quoi que tu appelle une "combinaison" ? et c'est les sommes de quoi ?

[Doraki]

Pour 8 bouteilles et 5 tests, c'est en effet impossible.

Chaque test doit comprendre 2 bouteilles (un test de 3 bouteilles sépare les 28 cas en 10+18, et 18>16 ; un test de 1 bouteille donne 28 -> 21+7)
Un test de 2 bouteilles donne 28 -> 15+13, et les deux sont <= 16 donc c'est le seul espoir.

Pour le choix de 2 tests, ça bloque : soit on ne met aucune bouteille en commun (28 -> 6+9+9+4, et 9>8), soit on en met 1 (28 -> 10+5+5+8, et 10>8)

Donc 2 tests ne peuvent pas séparer 28 en 4 catégories de maximum 8 cas chacun.

[nodjim]

Je me suis planté dans les sommes. Ici, ce ne sont pas des sommes ordinaires, on ne fait que cumuler les 1. Et donc un 7 par exemple masque 1,2,3,4,5,6. Comme dit Doraki, si on utilise 3 "1" pour 1 bouteille, ça limite les combis différentes, et ce n'est pas possible. Pareil si on désigne une bouteille par un seul "1".

[Doraki]

7 bouteilles en 5 tests est aussi impossible mais c'est un peu plus long à vérifier.
(en 6 tests c'est trivial en prenant 1 bouteille par test)