Coefficient directeur
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
smartynina
- Membre Naturel
- Messages: 53
- Enregistré le: 28 Fév 2008, 14:59
-
 par smartynina » 28 Jan 2012, 10:17
par smartynina » 28 Jan 2012, 10:17
Bonjour,
Je m'interroge sur la définition exacte du coefficient directeur d'une droite.
Est-il défini seulement pour les droites non verticales ou est-il égal à
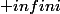
pour ces droites.
Merci
-
didou31
- Membre Relatif
- Messages: 230
- Enregistré le: 24 Sep 2008, 16:23
-
 par didou31 » 28 Jan 2012, 10:38
par didou31 » 28 Jan 2012, 10:38
Le coefficient directeur, c'est pour parler de manière imagée pas autre chose qu'une mesure de la pente d'une courbe. Autrement dit, il rend compte de l'élévation pour un déplacement horizontal unitaire.
La définition qui t'en a été faite en cours est exacte et complète.
Et effectivement, plus la droite se rapproche de la verticale et plus le coefficient directeur augmente et tend donc vers l'infini... ou vers - l'inifini. Autant dire que coefficient directeur n'est pas défini lorsqu'on évoque une droite "verticale". Mais, ce n'est pas un problème en soit.
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 28 Jan 2012, 10:43
par nodjim » 28 Jan 2012, 10:43
Une droite dans le plan est le résultat de la fonction y=ax+b, dont a est la pente ou le coefficient directeur. Plus a est grand et plus la droite sera proche de la verticale. La droite verticale se définit par la fonction x=constante.
-
smartynina
- Membre Naturel
- Messages: 53
- Enregistré le: 28 Fév 2008, 14:59
-
 par smartynina » 28 Jan 2012, 11:24
par smartynina » 28 Jan 2012, 11:24
Je suis entièrement d'accord avec vous, j'ai surement posté cette question dans la mauvaise partie du forum :
ce n'est pas la définition à donner à des lycéens qui mintéresse mais sa définition exacte. C'est à dire est-ce qu'il faut parler de coefficient directeur égal à
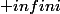
ou de non existence de ce coefficient pour les droites verticales.
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 28 Jan 2012, 11:31
par nodjim » 28 Jan 2012, 11:31
C'est, à y bien réfléchir, une question bien embarrassante...
Soit y=ax+b la droite et on veut trouver toutes les droites qui pivotent autour d'un pivot P situé sur l'axe des x.
yP=0 donc P=-b/a et donc b=-aP
Ces droites se réécrivent alors:
y=ax-aP et donc x=(y+aP)/a=y/a+P
Donc si a est infini, y/a=0 et x=P on a bien notre droite verticale.
Mais l'étrangeté est pour y= infini
x=1+P et ce x n'est plus sur la verticale!!!
Je ne vois pas de défaut dans cette démo..
Des avis ?
-
smartynina
- Membre Naturel
- Messages: 53
- Enregistré le: 28 Fév 2008, 14:59
-
 par smartynina » 28 Jan 2012, 11:49
par smartynina » 28 Jan 2012, 11:49
nodjim a écrit:C'est, à y bien réfléchir, une question bien embarrassante...
Soit y=ax+b la droite et on veut trouver toutes les droites qui pivotent autour d'un pivot P situé sur l'axe des x.
yP=0 donc P=-b/a et donc b=-aP
Ces droites se réécrivent alors:
y=ax-aP et donc x=(y+aP)/a=y/a+P
Donc si a est infini, y/a=0 et x=P on a bien notre droite verticale.
Mais l'étrangeté est pour y= infini
x=1+P et ce x n'est plus sur la verticale!!!
Je ne vois pas de défaut dans cette démo..
Des avis ?
Les droites qui pivotent autour de P sont de la forme y=a'x+b' où b'=-a'+b/a
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 28 Jan 2012, 12:17
par nodjim » 28 Jan 2012, 12:17
Les droites y=a(x-P) passent toutes par le point y=0 et x=P non ? et ce quelle que soit la valeur de a.
-
smartynina
- Membre Naturel
- Messages: 53
- Enregistré le: 28 Fév 2008, 14:59
-
 par smartynina » 28 Jan 2012, 12:33
par smartynina » 28 Jan 2012, 12:33
nodjim a écrit:Les droites y=a(x-P) passent toutes par le point y=0 et x=P non ? et ce quelle que soit la valeur de a.
Si j'ai bien compris votre raisonnement :
On part d'une droite d'équation y=ax+b. On fixe un point P qui est le point d'intersection de cette droite avec d'axe des abscisses.
Notons y=a'x+b' l'équation des droites passants par P. a' est forcément différent de a sinon les droites seraient parallèles.
Le point P passe par la droite d'équation y=a'x+b' on a donc une nouvelle expression de l'équation de la droite : y=a'(x-1)+b/a.
Après je suis un peu perdue dans ce que vous voulez faire.

-
Peacekeeper
- Membre Irrationnel
- Messages: 1408
- Enregistré le: 19 Jan 2012, 21:34
-
 par Peacekeeper » 28 Jan 2012, 12:35
par Peacekeeper » 28 Jan 2012, 12:35
nodjim a écrit:C'est, à y bien réfléchir, une question bien embarrassante...
Soit y=ax+b la droite et on veut trouver toutes les droites qui pivotent autour d'un pivot P situé sur l'axe des x.
yP=0 donc P=-b/a et donc b=-aP
Ces droites se réécrivent alors:
y=ax-aP et donc x=(y+aP)/a=y/a+P
Donc si a est infini, y/a=0 et x=P on a bien notre droite verticale.
Mais l'étrangeté est pour y= infini
x=1+P et ce x n'est plus sur la verticale!!!
Je ne vois pas de défaut dans cette démo..
Des avis ?
y est une ordonnée, elle ne peut être égale à infini, tout au plus peut-on la faire tendre vers l'infini. Et on a alors une forme indéterminée du type Infini/infini.
En tous les cas, ça ne me choque pas de dire qu'une droite verticale possède une pente infinie, je l'ai déjà entendu dire par des professeurs. D'ailleurs, on peut s'en convaincre en prenant 2 points quelconques A et B de la droite et calculer (yB-yA)/(xB-xA). Quelle que soit la valeur de yB-yA, on a xB-xA=0.
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 28 Jan 2012, 12:39
par nodjim » 28 Jan 2012, 12:39
Je ne comprends pas très bien pourquoi tu t'efforces d'ajouter a' et b'.
Simplifions le problème à l'extrême: Les droites y=ax passent toutes par le point (0;0).
a est un paramètre, celui de la pente. On peut donc dire que, pour l'ensemble des valeurs données à a, on a l'ensemble des droites qui passent par (0;0), autrement dit qui pivotent par (0;0).
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 28 Jan 2012, 12:46
par nodjim » 28 Jan 2012, 12:46
Peacekeeper a écrit:y est une ordonnée, elle ne peut être égale à infini, tout au plus peut-on la faire tendre vers l'infini. Et on a alors une forme indéterminée du type Infini/infini.
En tous les cas, ça ne me choque pas de dire qu'une droite verticale possède une pente infinie, je l'ai déjà entendu dire par des professeurs. D'ailleurs, on peut s'en convaincre en prenant 2 points quelconques A et B de la droite et calculer (yB-yA)/(xB-xA). Quelle que soit la valeur de yB-yA, on a xB-xA=0.
Ben oui, la pente infinie, c'est ce à quoi j'ai abouti. Et on raisonne bien avec toutes valeurs de y. A l'infini, x=1. Car pour cet infini, rien n'empêche de déclarer y=a.

-
Peacekeeper
- Membre Irrationnel
- Messages: 1408
- Enregistré le: 19 Jan 2012, 21:34
-
 par Peacekeeper » 28 Jan 2012, 12:50
par Peacekeeper » 28 Jan 2012, 12:50
nodjim a écrit: Car pour cet infini, rien n'empêche de déclarer y=a.
Je ne comprends pas très bien ce que tu veux dire. A l'infini, déclarer y=a? Donc a=ax+b? :s
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 28 Jan 2012, 12:55
par nodjim » 28 Jan 2012, 12:55
Peacekeeper a écrit:Je ne comprends pas très bien ce que tu veux dire. A l'infini, déclarer y=a? Donc a=ax+b? :s
y=ax donc x=a/y avec a qui est à l'infini.
tant que "y"a une valeur déterminée, x=0
Mais pour "y" à +l'infini alors x=1
Et pour "y" à -l'infini alors x=-1.

-
Peacekeeper
- Membre Irrationnel
- Messages: 1408
- Enregistré le: 19 Jan 2012, 21:34
-
 par Peacekeeper » 28 Jan 2012, 13:11
par Peacekeeper » 28 Jan 2012, 13:11
nodjim a écrit:y=ax donc x=a/y avec a qui est à l'infini.
tant que "y"a une valeur déterminée, x=0
Mais pour "y" à +l'infini alors x=1
Et pour "y" à -l'infini alors x=-1.
y=ax est l'équation d'une droite passant par l'origine du repère, or une droite verticale ne passe pas forcément par l'origine (d'ailleurs tu as fait une petite erreur d'inattention x=y/a

)
En plus, si tu dis que lorsque y est à l'infini x=1, ça veut dire que seule les droites x=1 et x=-1 sont verticales... :s
Infini/Infini est une forme indéterminée et n'est pas égal à 1.
Mais je suis d'accord sur le fait qu'une droite verticale est une droite de pente infinie, tout comme une droite horizontale est une droite de pente nulle.
-
smartynina
- Membre Naturel
- Messages: 53
- Enregistré le: 28 Fév 2008, 14:59
-
 par smartynina » 28 Jan 2012, 13:13
par smartynina » 28 Jan 2012, 13:13
Peacekeeper a écrit:y est une ordonnée, elle ne peut être égale à infini, tout au plus peut-on la faire tendre vers l'infini. Et on a alors une forme indéterminée du type Infini/infini.
En tous les cas, ça ne me choque pas de dire qu'une droite verticale possède une pente infinie, je l'ai déjà entendu dire par des professeurs. D'ailleurs, on peut s'en convaincre en prenant 2 points quelconques A et B de la droite et calculer (yB-yA)/(xB-xA). Quelle que soit la valeur de yB-yA, on a xB-xA=0.
Il semble que l'outil coefficient directeur a été introduit pour mesurer la croissance d'une droite. Du coup je trouve que parlais de coefficient directeur pour une droite verticale n'a pas dintérêt.
Finalement à quoi bon parler de pente infinie.
Par contre parler de coefficient directeur pour une droite horizontale a ici du sens : la fonction représenté est constante.
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 28 Jan 2012, 13:15
par nodjim » 28 Jan 2012, 13:15
Mettons pour l'indéterminé quand y tend vers l'infini, quoique je ne vois pas trop en quoi ces 2 infinis seraient différents.
On a donc bien là un curieux paradoxe:
On peut tracer la droite verticale aussi longue que l'on veut, mais on ne sait pas du tout ce qu'elle devient à l'infini....
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 28 Jan 2012, 13:19
par nodjim » 28 Jan 2012, 13:19
smartynina a écrit:Il semble que l'outil coefficient directeur a été introduit pour mesurer la croissance d'une droite. Du coup je trouve que parlais de coefficient directeur pour une droite verticale n'a pas dintérêt.
Finalement à quoi bon parler de pente infinie.
Par contre parler de coefficient directeur pour une droite horizontale a ici du sens : la fonction représenté est constante.
Tu as tout à fait raison, mais les Mathématiques se doivent d'être cohérentes. La pente infinie résulte simplement de l'équation de la droite. On ne peut donc pas mettre la droite verticale à part.
-
smartynina
- Membre Naturel
- Messages: 53
- Enregistré le: 28 Fév 2008, 14:59
-
 par smartynina » 28 Jan 2012, 13:23
par smartynina » 28 Jan 2012, 13:23
nodjim a écrit:Tu as tout à fait raison, mais les Mathématiques se doivent d'être cohérentes. La pente infinie résulte simplement de l'équation de la droite. On ne peut donc pas mettre la droite verticale à part.
Mais ça présuppose que le coefficient directeur est défini pour les droites verticales. S'il est défini, comme dans la plupart des ouvrages, seulement pour les droites non parallèles à l'axe des ordonnées, parler de pente infinie n'a plus lieu d'être.
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 28 Jan 2012, 13:26
par nodjim » 28 Jan 2012, 13:26
Le coefficient directeur pour les droites est défini, c'est l'infini.
-
smartynina
- Membre Naturel
- Messages: 53
- Enregistré le: 28 Fév 2008, 14:59
-
 par smartynina » 29 Jan 2012, 10:28
par smartynina » 29 Jan 2012, 10:28
nodjim a écrit:Le coefficient directeur pour les droites est défini, c'est l'infini.
Et dans quel ouvrage avez-vous trouvée cette définition ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités