Zéta (2)

par **titine** » 24 Nov 2006, 15:18

Bonjour,
il me semble que

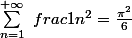
Mais, je ne sais plus comment on trouve ce résultat.
Merci.

par **yos** » 24 Nov 2006, 16:14

La méthode des séries de Fourier est la plus répandue. En version : "rien à savoir", ça donne :

On écrit 1/n² comme l'intégrale sur [0,pi] de (at+bt²)cos(nt) (a et b à choisir correctement).
On somme les intégrales de 0 à N et on utilise la formule

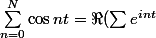qui se simplifie bien comme somme des termes d'une suite géométrique.
Enfin on fait tendre N vers l'infini.

par **tize** » 24 Nov 2006, 17:54

Je me suis posé la question il y a quelque mois et j'ai trouvé (entre autre) ceci
une idée de la preuve originale (Euler je crois - pas très rigoureuse) se trouve sur le site pi3,14

par **titine** » 25 Nov 2006, 14:23

Merci à vous 2 !

par **amine22** » 16 Mar 2007, 17:37

titine a écrit:Bonjour,
il me semble que

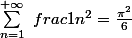
Mais, je ne sais plus comment on trouve ce résultat.
Merci.

salut
soit en utilusant les series du fourier ou en devlopent la serie entiére somme de x^2/n^2

Zéta (2)

Zéta (2)

amine

Qui est en ligne