En vrac: équa diff+ affine

[busard_des_roseaux]

Bs,

je pose mes questions en vrac:

i) pour les équa diffs linéaire à coefficients constants du 2ème ordre
la méthode de variations des constantes
conduit à poser:


et pour y', je ne me souviens plus


pour déterminer la solution générale.

?? je crois que Ben a traité du sujet récemment.

ii)
direction de la variété affine
ou n'importe quel s-e-v ?

[Ben314]

Une bonne façon de se rappeler les formules est de regarder une équa-diff d'ordre 2 (ou plus...) comme une équa-diff d'ordre 1 dont l'inconnue est le vecteur .
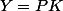
Lorsque tu as ta base de l'ensemble des solutions de l'équadiff. linéaire d'ordre 2 associée, cela signifie que les solutions (en vectoriel) sont les où est la matrice et où est un vecteur constant .

La méthode de variation de la constante consiste alors à considérer le vecteur comme variable.
Cela conduit bien aux deux équations que tu donne.

Dans la pratique, il faut aussi constater que :

donc la deuxième égalité : peut se récrire sous la forme équivalente : qui est utile pour la résolution

[alavacommejetepousse]

bonjour

en fait busard a écrit le contraire

la condition est bien celle de ben

A ' f1 + B' f2 = 0

on peut s en souvenir sans vectorialiser (sans wronskienniser) en se rappelant qu' à la fin on veut un système linéaire 2x2 en A ' et B'

donc pas de A" ni B" dans y " ce qui suggère ni A' ni B' dans y '

[busard_des_roseaux]

oui, tout à fait, je savais que ce que j'écrivais était faux. En effet, on cherche la solution générale. Il faut donc que résoudre en (A,B) soit équivalent à résoudre en y,y'..

ce qui impose qu'un déterminant , sans doute le Wronskien, ne puisse jamais s'annuler.Et ce déterminant est une exponentielle


dans le cas du deuxième ordre , c'est tout simplement
dont la non annulation vient de l'indépendance des solutions