Vous etes sur que vs ne pouvez pas m'aider?

[cplp2]

Bonjour,
J'ai un exercice sur la dualité mais je n'ai pas compris !
vraiment g tt essayé !!!
pouvez vous me donner quelques indications :
trouver 3 valeurs x, y, z positives rendant minimum l'expression 1320x + 350y + 900z et verifiant les conditions :
4x + y +2z > 100
3x + y + 3z > 120
Je vous remercie

[Chimerade]

Bonjour,
J'ai un exercice sur la dualité mais je n'ai pas compris !
vraiment g tt essayé !!!
pouvez vous me donner quelques indications :
trouver 3 valeurs x, y, z positives rendant minimum l'expression 1320x + 350y + 900z et verifiant les conditions :
4x + y +2z > 100
3x + y + 3z > 120
Je vous remercie

La zone qui t'intéresse est limitée par 5 plans, d'équations x=0, y=0, z=0, 4x+y+2z=100, 3x+y+3z=120. Tu dois dessiner cette zone, en en traçant les limites (des segments ou des demi-droites, intersections de ces cinq plans deux à deux). Donc tu dois d'abord les déterminer (les droites communes à deux plans) et ensuite les tracer : tu verras un peu mieux ce qui se passe. Ensuite, tu traceras un vecteur parallèle à (1320,350,900) et tu constateras que minimiser le produit (1320x+350y+900z) revient à minimiser le produit scalaire du vecteur (x,y,z) et de ce vecteur. En regardant la figure, tu peux (peut-être déterminer quel coin de la zone délimitée est le plus éloigné dans la direction opposée au vecteur (1320,350,900).

Pas facile à expliquer ! Mais fais d'abord le dessin, après tu réaliseras mieux ce que je dis !

[Chimerade]

Je précise...
On se place dans un repère orthonormé
Pour visualiser le plan P1 d'équation 4x + y + 2z = 100, il suffit de trouver trois points. Pourquoi pas trouver les points des axes ?
Si x=0, y=0 alors z=50. Ca nous donne le point A (0,0,50)
Si x=0, z=0 alors y=100. Ca nous donne le point B (0,100,0)
Si y=0, z=0 alors x=25. Ca nous donne le point C (25,0,0)
On trace les axes et les points A,B,C.
L'intersection de P1 avec le plan 0xy est la droite (BC)
L'intersection de P1 avec le plan 0yz est la droite (AB)
L'intersection de P1 avec le plan 0zx est la droite (CA)
Pour visualiser le plan P2 d'équation 3x + y + 3z = 120, il suffit de trouver trois points. Pourquoi pas trouver les points des axes ?
Si x=0, y=0 alors z=40. Ca nous donne le point D (0,0,40)
Si x=0, z=0 alors y=120. Ca nous donne le point E (0,120,0)
Si y=0, z=0 alors x=40. Ca nous donne le point F (40,0,0)
On trace les points D,E,F sur la figure.
L'intersection de P2 avec le plan 0xy est la droite (EF)
L'intersection de P2 avec le plan 0yz est la droite (DE)
L'intersection de P2 avec le plan 0zx est la droite (FD)

Sur la figure on voit que (AB) coupe (DE) dans le plan Oyz. Dans ce plan, l'équation de (AB) est :

Et l'équation de (DE) est :


Le point d'intersection des deux droites est le point G de coordonnées :
x=0,y=60, z=20

Sur la figure on voit que (AC) coupe (DF) dans le plan Oxz. Dans ce plan, l'équation de (AC) est :

Et l'équation de (DF) est :


Le point d'intersection des deux droites est le point H de coordonnées :
x=10,y=0, z=30

À présent observons la différence entre les expressions F(M) et F(M') de la fonction à minimiser
F(M)=1320x + 350y + 900z

F(M')-F(M) = 1320x' + 350y' + 900z' -(1320x + 350y + 900z)
F(M')-F(M) = 1320(x'-x) + 350(y'-y) + 900(z'-z)
Si l'on appelle le vecteur de coordonnées (1320,350,900) on voit que cette différence est égale à :


Il en résulte que F(M') sera inférieur à F(M) si et seulement si le produit scalaire est négatif.

D'où la méthode : on se place sur une limite quelconque du domaine "autorisé", par exemple en F. Et l'on va se déplacer le long de cette limite dans une direction définie par un vecteur tel que le produit scalaire soit négatif !

En partant de F trois directions privilégiées s'offrent à nous pour rester sur la limite de la zone "autorisée". Soit on part dans la direction de Ox (vecteur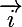 =1,0,0) soit on part vers E (vecteur = (-40,120,0)) soit on part vers D (vecteur = (-40,0,40)). Pour savoir dans quelle direction partir, il suffit d'en choisir une pour laquelle le produit scalaire est négatif :




En effet le point G ne respecte pas ces contraintes puisque pour ce point :


On peut choisir un point "proche de G" pour que les inégalités soient strictes, mais ce ne sera pas un minimum car on peut toujours en trouver un autre pour lequel l'expression "1320x + 350y + 900z" sera plus petite. Dans la pratique, on a plutôt des inégalités larges, de sorte qu'il existe bien un minimum, qui, ici, est bien G.

[sept-épées]

diable! ça, c'est de la réponse détaillée...