Volumes de rotation

[4square]

Bonjour,

Je voudrais demander lors de l’utilisation de la méthode du disque, pourquoi le surface de la zone située entre la courbe 4x²+y²=16 (une ellipse) et l’axe x crée un volume de rotation, autour de l’axe x, est-il égal au double du volume pour la même courbe lorsqu’il est tourné autour de l’axe y ?

Merci d'avance.

[GaBuZoMeu]

Bonjour,

Pour obtenir une sphère de rayon 4, on dilate par 2 sur un axe dans le premier cas et on dilate par 2 sur deux axes dans le deuxi_me cas.

[4square]

[][/img]

[GaBuZoMeu]

Allo ?

[4square]

J'ai voulu attacher un document mais pas de chance, donc voici le problème:
Ellipse = 4x²+y²=16
(1) rotation axis x: y²=16-4x², pi.integral de16-4x².dx entre 2 et -2 =Volume = π.128/3
(2) rotation axis y: x²=4-(y²/4), pi.integral de 4-(y²/4).dx entre 4 et -4=Volume = π.64/3

Pourquoi il y a un différence entre les deux résultats ?

[GaBuZoMeu]

Je t'ai expliqué pourquoi la différence et pourquoi le rapport entre les deux. Tu n'as pas lu ?
En plus mon explication donne sans calcul les résultats que tu trouves, si tu connais le volume d'une sphère de rayon 4.

[4square]

Oui, merci je l'avais lu et évidemment je n'ai pas compris - je pense que s'agit d'une ellipse ?

[GaBuZoMeu]

Les volumes sont des ellipsoïdes de révolution.
Je pensais que tu savais qu'une dilatation de facteur k sur un axe multiplie le volume pas k.

[4square]

Bonjour,

Merci pour votre réponse et intéresse - je n'ai pas compris votre solution: "Les volumes sont des ellipsoïdes de révolution. Je pensais que tu savais qu'une dilatation de facteur k sur un axe multiplie le volume pas k."

Avez vous compris ma question ? Peut-être je n'étais pas clair ?

Avez vous fait le graphique du courbe ? pour moi ça donne une ellipse.

Si on utilise les méthode disc pour le x et y axe on a deux résultats différents - pour quoi ? quand on peut imaginer le volume crée, en faisant tourner l’ellipse autour de l’axe x ou l’axe y, doit donner le même volume; L’ellipse étant centrée sur les coordonnées (0,0).

Avez vous essayé de faire le analyse ?

Cordialement.

[Ben314]

Salut,

Avez vous compris ma question ? Peut-être je n'étais pas clair ?

Oui, il a parfaitement compris la question et . . . parfaitement répondu . . .

Avez vous fait le graphique du courbe ? pour moi ça donne une ellipse.

Une soit disant "éllipse" dont on calcule (selon toi) le "volume", ça n'a évidement pas de sens. Une ellipse, c'est une courbe plane qui délimite une surface (donc on peut parler de son aire). Et si tu prend le même type d'équation, mais en dimension 3, donc un truc de la forme (avec des constantes strictement positives fixées), là, c'est une surface qui délimite bien un volume, et ça s'appelle un "ellipsoïde" (de révolution si deux des trois axes sont de même longueur).

Si on utilise les méthode disc pour le x et y axe on a deux résultats différents - pour quoi ?

Tout simplement parce qu'il n'y a aucune raison particulière qu'on obtienne la même chose !!!
Si je fait tourner l'objet le plus simple qui me vienne à l'esprit, à savoir un rectangle centré sur l'origine du repère, alors quand je le fait tourner autour de l'axe des x ou de l'axe des y, dans les deux cas, j'obtient un cylindre, mais les deux cylindres n'ont pas le même volume (sauf si le rectangle est carré, bien sûr).
Vérifie.

[GaBuZoMeu]

quand on peut imaginer le volume crée, en faisant tourner l’ellipse autour de l’axe x ou l’axe y, doit donner le même volume

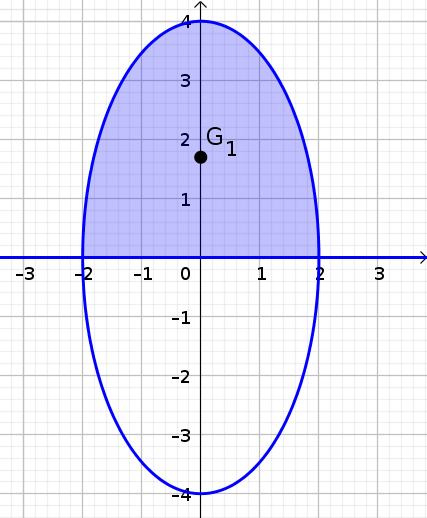
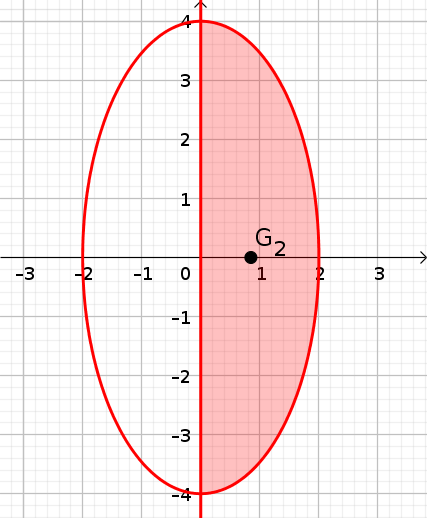
Ça c'est une idée complètement fausse, comme l'a déjà dit Ben314. Un solide de révolution est engendré par une surface plane tournant autour d'un axe situé dans son plan et ne coupant pas cette surface. Dans les deux cas présents la surface qui engendre le volume de révolution est la moitié du demi-disque elliptique de grand axe 8 (porté par l'axe des y) et de petit axe 4 (porté par l'axe des x) ; dans le premier cas on prend le demi-disque elliptique coupé par l'axe des x et on fait tourner autour de cet axe, dans le deuxième cas on prend le demi-disque coupé par l'axe des y qu'on fait tourner autour de l'axe des y.,
Tu penses que les volumes des solides de révolution doivent être les mêmes puisque les demi-disques elliptiques qui les engendrent ont même aire. Mais ces volumes dépendent aussi de la distance du centre de gravité de la surface génératrice à l'axe de rotation. Je te renvoie au deuxième théorème de Guldin que tu peux trouver ici : https://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8mes_de_Guldin#Second_%C3%A9nonc%C3%A9. Le volume du solide de révolution est le produit de l'aire de la surface génratrice par fois la distance du centre de gravité de cette surface à l'axe de révolution.
Dans le cas qui nous occupe, vu que le grand axe est deux fois plus grand que le petit axe, la distance du centre de gravité du demi-disque découpé par le petit axe à ce petit axe est deux fois plus grande que la distance du centre de gravité du demi-disque découpé par le grand axe à ce grand axe :

[GaBuZoMeu]

[GaBuZoMeu]

[4square]

Merci à Ben314 et GaBuZoMeu,

Je bien compris mon erreur et ce que vous avez expliqué.

Je dois (malheureusement) admettre que j’étais fixé sur l’idée que les 2 volumes de révolution auraient le même volume... Complètement faux bien sûr - j’étais aveugle aux deux volumes différents que l’ellipse créerait en rotation autour des deux axes différents. Toutes mes excuses!