[Résolu] Volume Pyramide

[Melkor]

Bonjour à tous,
j'ai un petit souci pour le calcul du volume d'une pyramide
J'ai bien trouvé un "truc" mais je crains que ce ne soit qu'une magouille de physicien pour arriver à mes fins et je voudrais avoir votre avis si la démarche est correcte ou pas.

Pyramide à base carrée de côté c et de hauteur h.


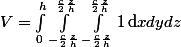
Bon on voit pas très bien les bornes intégrales, mais c'est de -cz/2h à cz/2h pour les deux dernières intégrales (intégrale de 1dx et intégrale de 1dy).

Puis j'intègre par rapport à z de 0 à h c²z²/h² et je retrouve bien la formule B.h/3 mais c'est sans doute un coup de chance que ça marche.

Merci de votre avis :++:

[Finrod]

malgré l'antagonisme évident de nos pseudo, je vais essayer de répondre.

En même temps, je ne vais pas m'étendre. C'est juste.

La différence entre une magouille de physicien et une preuve mathématiques est sans doute que le mathématicien doit expliquer en détail et rigoureusement.

Après tout on peut avoir le bon résultat avec une démarche fausse.

[Melkor]

c'est vrai, mais en vérité ce que je cherche c'est de calculer des matrices d'inertie, et comme x² y² et z² interviennent, les bornes des intégrales deviennent déterminantes.
Malheureusement je n'ai pas trouvé d'exercices avec des solutions pour vérifier si mes calculs sont justes :/

(Pour le pseudo, il est grand temps que je lise le Silmarillion pour enfin comprendre toutes les allusions au miens :D)

[ToToR_2000]

Ta démarche est tout à fait correcte pour calculer le volume.
Tu peux également voir le calcul du volume de cette façon (ça revient au même qu'a la tienne):
On découpe la pyramide horizontalement (càd // au plan xOy) pour avoir des tranches de hauteur infinitésimale dz qu'on peut assimiler à des pavés de hauteur dz et surface l(z)*l(z) où l(z) est la longueur du pavé (mais aussi la largeur) à l'altitude z.
Le volume est donc l'intégrale sur z de 0 à h de l(z)^2.
Reste à trouver l(z).
Pour ça, tu prends une des face triangulaires de la pyramide et tu appliques le th. de Thalès pour voir ce que vaut l(z) (=z/h).

[Melkor]

ouki merci :++: