Volume paraboloïde
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 29 Déc 2010, 19:21
par Dinozzo13 » 29 Déc 2010, 19:21
Bonsoir, j'ai un petit soucis pour trouver un volume.
Soit
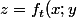=t-x^2-y^2, t\ge 0)
, je cherche en fait le volume du paraboloïde
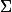
situé au-dessus du plan (O;(Ox),(Oy)).
J'ai pensé que c'était en calculant
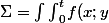 \quad dxdy)
, mais je ne vois pas comment la calculer, merci de m'aider.
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 29 Déc 2010, 19:28
par XENSECP » 29 Déc 2010, 19:28
Je dirais qu'il te manque une intégrale... dx dy dt
Après bah si tu coupes l'intégrale en 3, ça doit se faire non ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 29 Déc 2010, 19:38
par Dinozzo13 » 29 Déc 2010, 19:38
Oui, sauf que le terme t est un paramètre et est supposé fixe donc je ne pense pas qu'il faille le traiter comme une variable. Sinon, peux-tu me guider dans le calcul de ce volume.
(Ne va pas trop vite, je découvre les intégrales double et triple :++:)
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 29 Déc 2010, 19:45
par Arnaud-29-31 » 29 Déc 2010, 19:45
Salut Dinozzo !
On est d'accord qu'on a affaire au paraboloïde classique
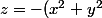)
dirigé vers le bas et décalé d'une distance t suivant z.
Si je considère le cercle obtenu par l'intersection du plan z = cste (

)
alors ce cercle à pour rayon
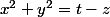
. Son aire vaut
^2)
.
Il ne reste plus qu'à intégrer pour z allant de 0 à t le cylindre élémentaire de base le cercle en question et d'épaisseur dz.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 29 Déc 2010, 19:50
par Dinozzo13 » 29 Déc 2010, 19:50
oui, entièrement d'accord, donc, (je sais pas si on peux l'écrire mais) :
 \quad dxdy = {\int}_0^t {\pi(t-z)^2 } \quad dz)
?
Je calcule cette intégrale et je te tiens au courant, merci :+++:
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 29 Déc 2010, 19:52
par XENSECP » 29 Déc 2010, 19:52
Dinozzo13 a écrit:Oui, sauf que le terme t est un paramètre et est supposé fixe donc je ne pense pas qu'il faille le traiter comme une variable. Sinon, peux-tu me guider dans le calcul de ce volume.
(Ne va pas trop vite, je découvre les intégrales double et triple :++:)
Hum ok autant pour moi ! C'est juste que dans ton intégrale il y a un 0 et un t qui traînent donc bon !
Les autres ont répondu donc je sors du sujet

-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 29 Déc 2010, 19:58
par Dinozzo13 » 29 Déc 2010, 19:58
Attention, j'ai crée cette intégrale pour répondre à un problème, je n'ai jamais dit qu'elle était correcte pour ce calcul.
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 29 Déc 2010, 19:59
par Arnaud-29-31 » 29 Déc 2010, 19:59
Ca n'a pas vraiment de sens ton intégrale de gauche ...
Après si tu veux passer par l'intégrale triple, le problème se prête mieux à une étude en coordonnées cylindriques :
Un volume élémentaire s'écrit
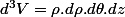
Donc
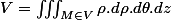
et on détermine les bornes :

(et
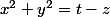
),

et

Notre intégrale est donc
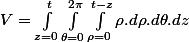
qui en deux ligne nous fait retomber sur l'intégrale que je t'ai proposé.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 29 Déc 2010, 20:05
par Dinozzo13 » 29 Déc 2010, 20:05
Oui, mais je n'ai pas vu les coordonnées cylindriques malheureusement.
Sinon je trouve
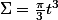
, est-ce bon ?
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 29 Déc 2010, 21:12
par Arnaud-29-31 » 29 Déc 2010, 21:12
Oui ca m'a l'air pas mal :)
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 30 Déc 2010, 20:26
par Dinozzo13 » 30 Déc 2010, 20:26
Au pire, si tuu pouvais me donner un moyen de vérifier, pour en être sûr.
Dans ce cas-ci la surface est particulière mais si dans un autre exemple on a pas de disque mais plutôt un truc bizarre, là il faut calculer l'aire avec une intégrale ?
Si tu veux m'expliquer ça, tu pourras prendre un exemple.
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 30 Déc 2010, 21:18
par Arnaud-29-31 » 30 Déc 2010, 21:18
Quand j'ai dis ca a l'air pas mal, ca voulait dire oui c'est bien ça ^^
La comme la surface est particulière, j'ai pu me ramener directement à une intégrale simple ...
Si la surface est un truc bizarre et que l'on arrive pas a voir quoi intégrer, on peut revenir à l'intégrale triple.
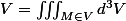
Qui peut se traduire suivant différents systèmes de coordonnées :
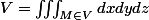
en cartésiennes
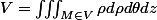
en cylindrique
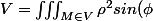d\rho d\theta dz)
en sphérique
Le travail consiste à chercher les bornes (de x, y et z en cartésiennes)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités