Vecteurs

par **Bloodthirsty** » 03 Déc 2012, 17:19

Salut tout le monde j'ai un p'tit exercice à rendre et j'aurais besoin de vos conseils :

M, A, B, C étant 4 points du plan, montrer que vecteur(BC)=vecteur(AC)-vecteur(AB).

Relation de Chasles : vecteur(BC) = vecteur(BA)+vecteur(AC)
= - vecteur(AB) + vecteur(AC)

Pour ça je pense avoir bon mais pour la suite je suis un peu plus perdu :

En déduire vecteur(MA).vecteur(BC) + vecteur(MB).vecteur(CA)+vecteur(MC).vecteur(AB) = 0

Merci d'avance, bonne soirée.

par **chan79** » 03 Déc 2012, 17:52

Bloodthirsty a écrit:Salut tout le monde j'ai un p'tit exercice à rendre et j'aurais besoin de vos conseils :

M, A, B, C étant 4 points du plan, montrer que vecteur(BC)=vecteur(AC)-vecteur(AB).

Relation de Chasles : vecteur(BC) = vecteur(BA)+vecteur(AC)
= - vecteur(AB) + vecteur(AC)

Pour ça je pense avoir bon mais pour la suite je suis un peu plus perdu :

En déduire vecteur(MA).vecteur(BC) + vecteur(MB).vecteur(CA)+vecteur(MC).vecteur(AB) = 0

Merci d'avance, bonne soirée.

Salut
Remplaces

par

+

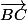
par

+

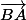
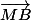
par

+

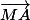
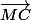
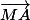
par **Bloodthirsty** » 03 Déc 2012, 18:14

Merci à toi, juste pour confirmer, si M est l'intersection de deux des trois hauteurs du triangle ABC, c'est bien le centre de gravité en M de celui-ci ?

par **chan79** » 03 Déc 2012, 19:57

Bloodthirsty a écrit:Merci à toi, juste pour confirmer, si M est l'intersection de deux des trois hauteurs du triangle ABC, c'est bien le centre de gravité en M de celui-ci ?

non, c'est ce qu'on appelle l'orthocentre du triangle ABC

par **Bloodthirsty** » 03 Déc 2012, 21:01

Ah ok, merci à toi pour ton aide, bonne fin de soirée ! :)

par **Bloodthirsty** » 04 Déc 2012, 17:25

je reviens juste pour une question de l'autre partie indépendante de mon exercice : Soit vect(a) un vecteur du plan et c un réel. Trouver un vecteur vect(0) colinéaire à vect(a) tel que vect(a).vect(0) = c.
Je comprend pas ce qu'on me demande si quelqu'un à une idée.

++

par **chan79** » 04 Déc 2012, 20:09

Bloodthirsty a écrit:je reviens juste pour une question de l'autre partie indépendante de mon exercice : Soit vect(a) un vecteur du plan et c un réel. Trouver un vecteur vect(0) colinéaire à vect(a) tel que vect(a).vect(0) = c.
Je comprend pas ce qu'on me demande si quelqu'un à une idée.

++

utilise la formule

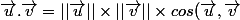le cosinus est égal à 1 ou -1

par **Bloodthirsty** » 04 Déc 2012, 22:50

Ca marche, merci

par **Bloodthirsty** » 04 Déc 2012, 23:12

Je trouve V0= c/(a x cos(vect(a),vect(0)) c'est ça ?

par **Bloodthirsty** » 05 Déc 2012, 14:07

Un petit Up ?

par **chan79** » 05 Déc 2012, 15:31

Bloodthirsty a écrit:Un petit Up ?

= k.

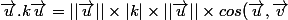= c
si c est positif, le cosinus est égal à 1 ( car il ne peut est égal qu'à 1 ou -1) donc k=

si c est négatif ...

par **Bloodthirsty** » 05 Déc 2012, 16:42

le cosinus est égal à -1 donc k = - c/ //u//^2 ou impossible ?

par **chan79** » 05 Déc 2012, 18:32

Bloodthirsty a écrit:le cosinus est égal à -1 donc k = - c/ //u//^2 ou impossible ?

Si c est positif on a un vecteur

de même sens que

sinon, il est de sens contraire

par **Bloodthirsty** » 05 Déc 2012, 19:29

Très bien, merci pour ton aide, bonne soirée :)

Vecteurs

Vecteurs

Qui est en ligne