Bonjour,
J'aurais plusieurs questions concernant l'indépendance de variables et vecteurs aléatoires.
1) Si (Xn)n est une suite de v.a indépendantes alors est-ce juste de dire que (X1,X2,..X_(n-1)) est indépendant de Xn?
J'ai essayé de le prouver mais je ne suis pas sûre que ce soit juste :
Soit
_n)
une suite de v.a.r indépendantes. On note
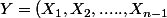)
. Calculons
)
avec
)
et
)
. Alors
 = P( X_1 \in A_1, X_2 \in A_2,....,X_{n-1} \in A_{n-1}, X_n \in B) = P(X_1 \in A_1).P(X_2 \in A_2).........P(X_n \in B))
ce qui prouve que

et

sont indépendantes.
Est ce qu'on peut généraliser un peu, en disant que si

et

sont de vecteurs aléatoires dont les composantes sont des

(en supposant de plus qu'ils n'ont aucune composante en commun) alors ils sont indépendants?
2) Si j'ai une v.a constante, est-elle indépendantes de n'importe quelle autre v.a? vecteur aléatoire?
3) Si

et

sont deux vecteurs aléatoires aléatoires indépendants (pas forcément de même dimension), cela implique t-il que les toutes les composantes de Y soient indépendantes de toutes celles de Z?
