Moi je sais que
Vecteur unitaire
13 messages
- Page 1 sur 1
vecteur unitaire
par samo12 » 04 Mar 2014, 13:26
Bonjour,
Moi je sais quee_x+cos(\theta)e_y)
Mais c'est quoi le , z'\in R^3)
merci de m'éclaircir.
Moi je sais que
par barbu23 » 04 Mar 2014, 13:49
Bonjour, :happy3:
Tu sais ce que c'est que fibré vectoriel ? :hein:
Si les éléments de la base , e_{\theta} (z) \})
dépend d'une variable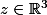 
, cela signifie que 
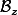est une base du fibré vectoriel 
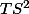( fibré vectoriel d'un cercle ici ) qui est l'ensemble des couples  + \beta e_\theta (z) ) \ | \ z \in S \ , \ e_{r} (z) , e_{\theta} (z) \in T_z S^2 \} \simeq S \times V)
avec 
un espace vectoriel de dimension 
engendré par  , e_{\theta} (z)} \})
Bref un fibré vectoriel est une famille d'espaces vectoriels qui dépend , ainsi que leurs base, d'un paramètre
de manière continue et non discret.
Cordialement.
Tu sais ce que c'est que fibré vectoriel ? :hein:
Si les éléments de la base
Bref un fibré vectoriel est une famille d'espaces vectoriels qui dépend , ainsi que leurs base, d'un paramètre
Cordialement.
par barbu23 » 04 Mar 2014, 14:27
samo12 a écrit:Re,
Merci mais que peut-on dire de?
Si
Cordialement. :happy3:
par samo12 » 04 Mar 2014, 14:30
Désolé, je vois pas ce vous venez de dire, donc on peut pas calculer ce produit scalaire?
par barbu23 » 04 Mar 2014, 14:31
Je viens de modifier mon message, relis ce que j'ai écrit. :happy3:
par samo12 » 04 Mar 2014, 14:48
Je voulais dire quand est ce que les deux vecteurs sont colinéaires?
par barbu23 » 04 Mar 2014, 15:02
samo12 a écrit:Je voulais dire quand est ce que les deux vecteurs sont colinéaires?
Excuse moi, je dois partir, je suis hyperpréssé, reviens dans
Toutes mes excuses. :happy3:
par barbu23 » 04 Mar 2014, 19:34
Re - bonjour,
Je suis un peu perdu devant ce grand nombre de notations que je n'arrive pas à les ordonner dans mon esprit :
Si j'ai bien compris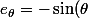 e_x + \cos ( \theta ) e_{y})
, non ?
Pour ne pas se perdre, on va aller étape par étape :
On définit d'abord la surface parametrée de dimension
dans 
qui représente le cercle unité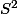 
, par :
 = ( \cos ( \theta ) , \sin ( \theta ) ))
Alors :)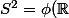
est le cercle unité.
Le vecteur tangent à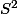 en est :  = d \phi ( \theta ) . 1 = \phi ' (\theta) = ( - \sin ( \theta ) , \cos ( \theta ) ))
Donc, pour et 
deux points sur le cercle tels que )
et )
sont respectivement les vecteurs tangents à 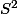en ces deux points et .
Donc : = ( - \sin ( \theta_1 ) , \cos ( \theta_1 )))
et  = ( - \sin ( \theta_2 ) , \cos ( \theta_2 ) ))
Par conséquent, les produit scalaire de ces deux vecteurs est :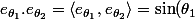 \sin ( \theta_2 ) + \cos ( \theta_1 ) \cos ( \theta_2 ) = \cos ( \theta_1 - \theta_2 ))
Donc, pour que)
et )
soient colinéaire, il faut que le produit scalaire :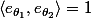 
C'est à dire, si : = 1)
C'est à dire, si :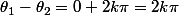
avec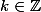 
C'est à dire, si :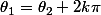
avec .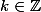
Cordialement. :happy3:
Je suis un peu perdu devant ce grand nombre de notations que je n'arrive pas à les ordonner dans mon esprit :
Si j'ai bien compris
Pour ne pas se perdre, on va aller étape par étape :
On définit d'abord la surface parametrée de dimension
Alors :
Le vecteur tangent à
Donc, pour
Donc :
Par conséquent, les produit scalaire de ces deux vecteurs est :
Donc, pour que
C'est à dire, si :
C'est à dire, si :
C'est à dire, si :
Cordialement. :happy3:
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 18 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :