Vecteur non gaussien à composantes gaussiennes

[melreg]

Re-Bonjour,

Je sèche à nouveau...

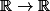
Trouver une fonction g: et C>0 t.q.

soit la densité d'un vecteur gaussien de , dont les lois marginales sont gaussiennes.

J'ai d'abord pensé prendre g impair (en prenant garde à ce qu'elle soit intégrable)pour faire disparaître le terme g(x)g(y) (quand on intégre pour trouver la loi marginale). Il faut alors faire attention à ce que f soit positive p.p. puis fixer C pour que. Mais quand je regarde l'intégrale de la loi marginale...elle ne vaut pas 1!

:help:

Merci d'avance

Remarque : La motivation de cet exo est la suivante: si on a un vecteur gaussien, la loi marginale de ses composantes est gaussienne. Cet exo montre que la réciproque est fausse!

[melreg]

Visiblement, je n'ai pas réussi à vous captiver...