bojour
je cherche la définition d'une variété affine ,et comment je peut monter qu'un sous ensemble d'un espace affine est une variété affine
merci.
Variété affine
7 messages
- Page 1 sur 1
c'est la même chose qu'un sous espace affine
E l espace affine E flèche l espace vectoriel sous jacent
F est un sea de E s 'il existe A ds F et F flèche sev de E flèche tel que
{vecteur AB avec B dans F } = F flèche.
on écrit alors F = A + F flèche
[REM A ne joue pas de rôle particulier pour B ds F
F = B + F flèche]
donc suffit de montrer que {vecteur AB, B dans F} est un sev de E flèche.
un sea s'identifie à un sev moyennement le choix d'un point A du sea.
E l espace affine E flèche l espace vectoriel sous jacent
F est un sea de E s 'il existe A ds F et F flèche sev de E flèche tel que
{vecteur AB avec B dans F } = F flèche.
on écrit alors F = A + F flèche
[REM A ne joue pas de rôle particulier pour B ds F
F = B + F flèche]
donc suffit de montrer que {vecteur AB, B dans F} est un sev de E flèche.
un sea s'identifie à un sev moyennement le choix d'un point A du sea.
Bonjour,
D'après wikipedia, une variété affine est une partie de E stable par prise de barycentre, et c'est équivalent à « sous-espace affine ».
D'après wikipedia, une variété affine est une partie de E stable par prise de barycentre, et c'est équivalent à « sous-espace affine ».
Ton espace ambiant est l'espace affine  dont l'espace vectoriel sous-jacent est
dont l'espace vectoriel sous-jacent est  (vu comme espacec vectoriel). Une partie D de
(vu comme espacec vectoriel). Une partie D de  est un espace affine si, quand tu fixes un point A de D l'ensemble des vecteurs
est un espace affine si, quand tu fixes un point A de D l'ensemble des vecteurs 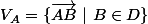 est un sous espace vectoriel de
est un sous espace vectoriel de  . Dans ce cas la dimension du sous espace vectoriel est la dimension du sous espace affine.
. Dans ce cas la dimension du sous espace vectoriel est la dimension du sous espace affine.
Dans ton cas, prends un point (au hasard) dans ton espace et calcul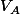 .
.
Dans ton cas, prends un point (au hasard) dans ton espace et calcul
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
